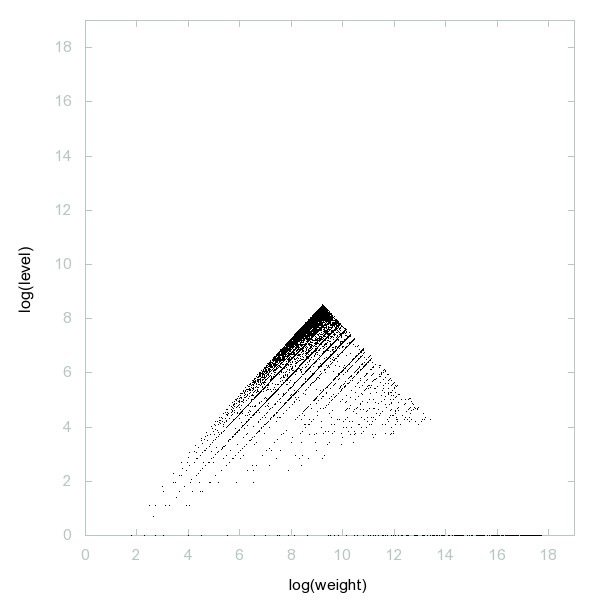
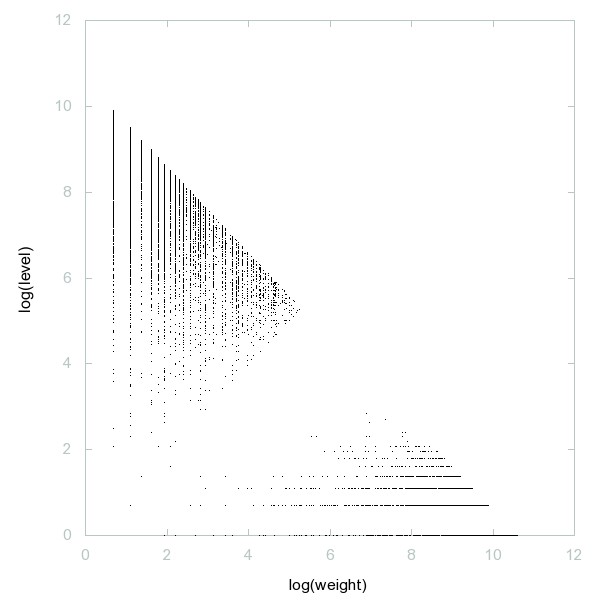
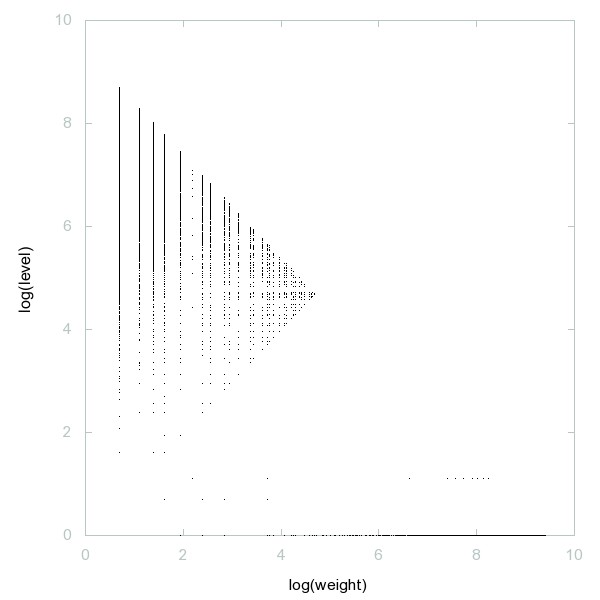
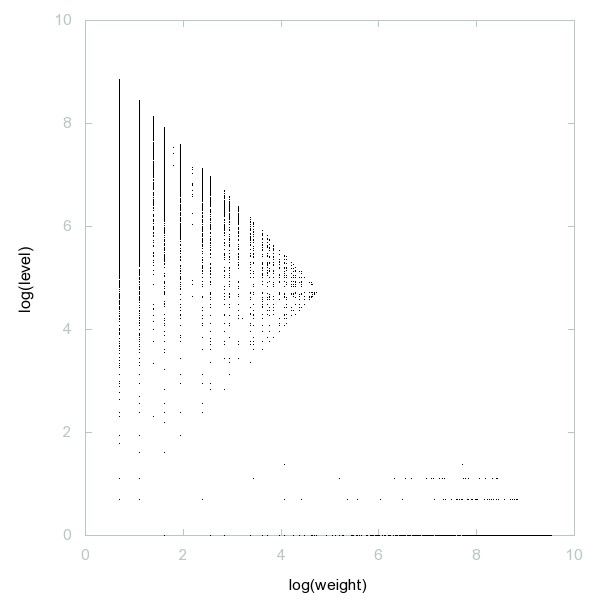
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of Central polygonal numbers

3D graph (WebGL) / 2D graph - First 500 terms
Central polygonal numbers (the Lazy Caterer's sequence): n(n+1)/2 + 1; or, maximal number of pieces formed when slicing a pancake with n cuts.
A000124(n) = A000000(n) * A000000(n) + (n + 1)
Download CSV of the decomposition of Central polygonal numbers (10000 lines.)
Decomposition of Central polygonal numbers - 9997 dots.

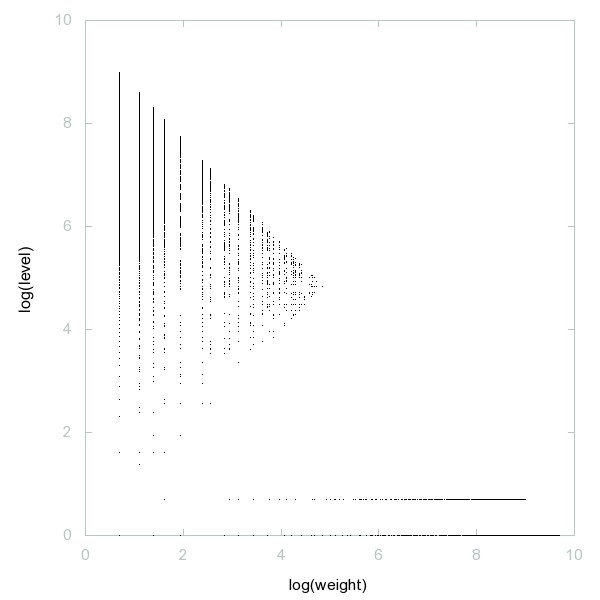
Decomposition of Lower Wythoff sequence

3D graph (WebGL) / 2D graph - First 500 terms
Lower Wythoff sequence (a Beatty sequence): a(n) = floor(n*phi), where phi = (1+sqrt(5))/2.
A000201(n) = A000000(n) * A000000(n) + A014675(n)
Download CSV of the decomposition of Lower Wythoff sequence (9999 lines.)
Decomposition of Lower Wythoff sequence - 9997 dots.

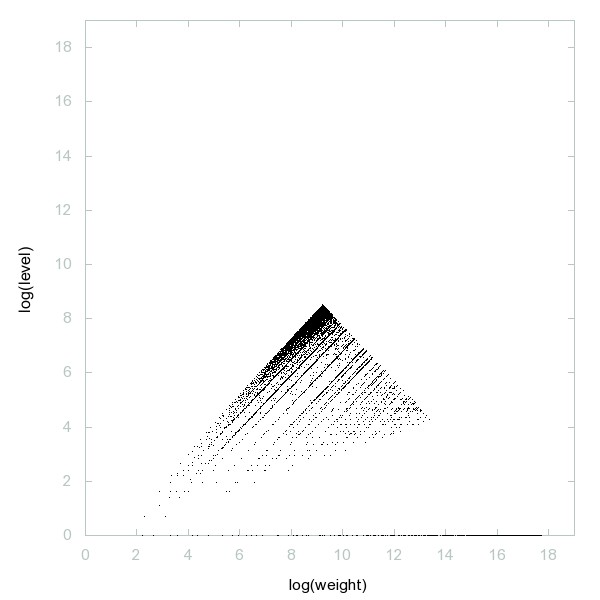
Decomposition of Triangular numbers

3D graph (WebGL) / 2D graph - First 500 terms
Triangular numbers: a(n) = C(n+1,2) = n(n+1)/2 = 0+1+2+...+n.
A000217(n) = A130703(n) * A184219(n) + (n + 1)
Download CSV of the decomposition of Triangular numbers (10000 lines.)
Decomposition of Triangular numbers - 9996 dots.

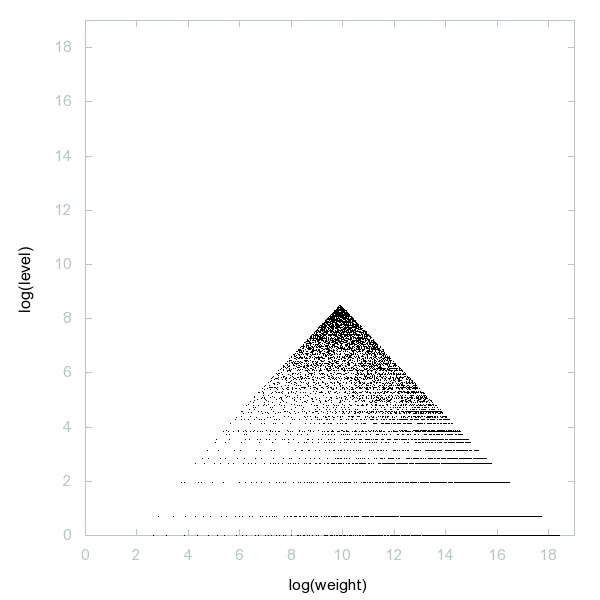
Decomposition of Squares

3D graph (WebGL) / 2D graph - First 500 terms
The squares: a(n) = n^2.
A000290(n) = A133150(n) * A184221(n) + A005408(n)
Download CSV of the decomposition of Squares (10000 lines.)
Decomposition of Squares - 9996 dots.

Decomposition of A000378

3D graph (WebGL) / 2D graph - First 500 terms
Numbers of the form x^2 + y^2 + z^2 (x, y, z >= 0).
A000378(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A000378 (9999 lines.)
Decomposition of A000378 - 9996 dots.

Decomposition of A000379

3D graph (WebGL) / 2D graph - First 500 terms
A 2-way classification of integers: complement of A000028.
A000379(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A000379 (9999 lines.)
Decomposition of A000379 - 9998 dots.

Decomposition of A000404

3D graph (WebGL) / 2D graph - First 500 terms
Numbers that are the sum of 2 nonzero squares. (seq not found)
A000404(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A000404 (9999 lines.)
Decomposition of A000404 - 9997 dots.

Decomposition of A000408

3D graph (WebGL) / 2D graph - First 500 terms
Numbers that are the sum of 3 nonzero squares.
A000408(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A000408 (9999 lines.)
Decomposition of A000408 - 9997 dots.

Decomposition of A000415

3D graph (WebGL) / 2D graph - First 500 terms
Numbers that are the sum of 2 but no fewer nonzero squares.
A000415(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A000415 (9999 lines.)
Decomposition of A000415 - 9997 dots.

Decomposition of A000452

3D graph (WebGL) / 2D graph - First 500 terms
a(n) is smallest number which avoids any 3-term geometric progression.
A000452(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A000452 (9999 lines.)
Decomposition of A000452 - 9996 dots.