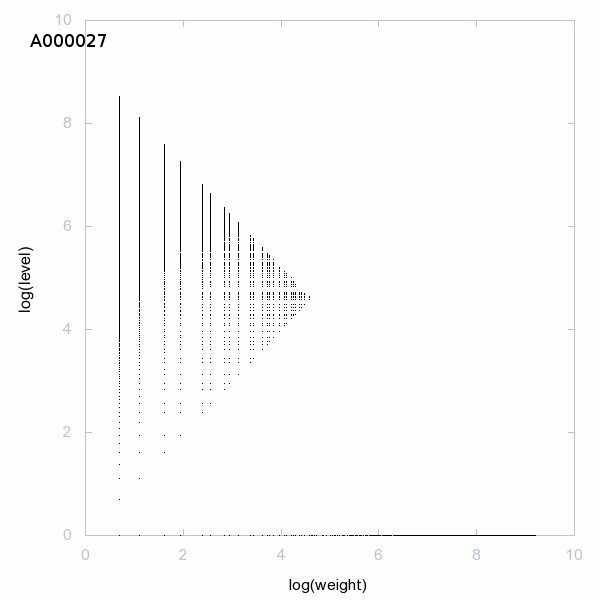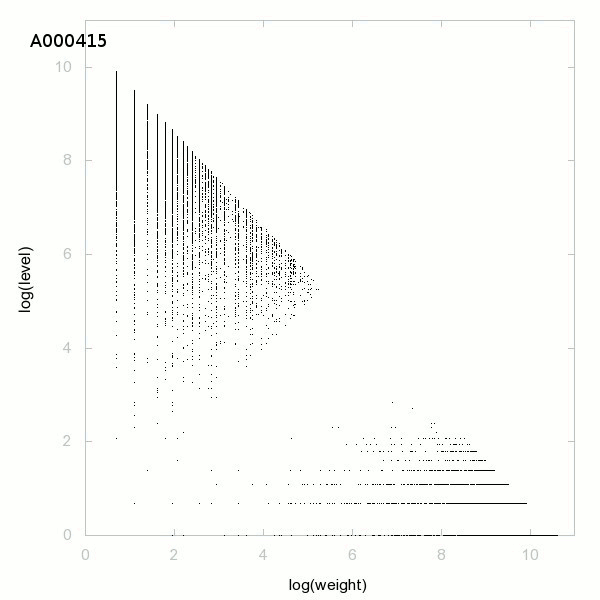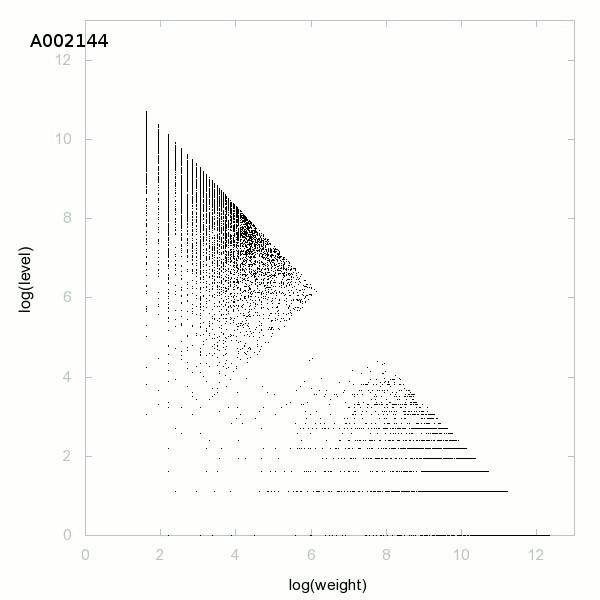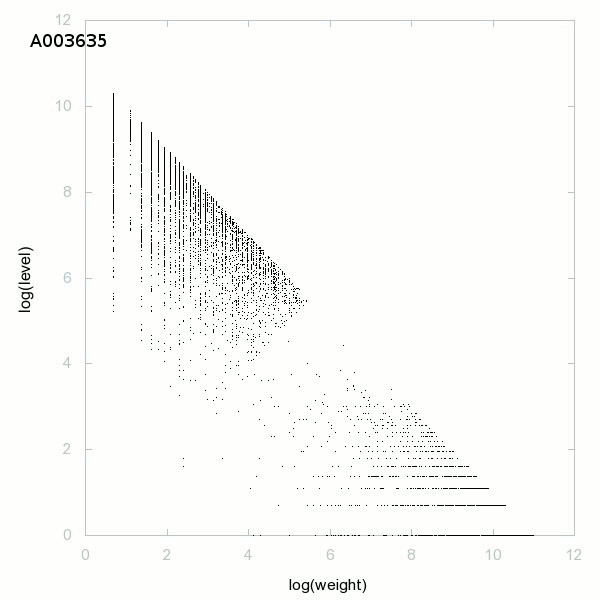
Decomposition into weight × level + jump - 3D graphs - 2D graphs - First 500 terms
The decomposition into weight × level + jump is a decomposition of positive integers. The weight is the smallest such that in the Euclidean division of a number by its weight, the remainder is the jump (first difference, gap). The quotient will be the level. So to decompose a(n), we need a(n+1) with a(n+1)>a(n) (strictly increasing sequence), the decomposition is possible if a(n+1)<3/2×a(n) and we have
a(n) = weight × level + jump.
We see the fundamental theorem of arithmetic and the sieve of Eratosthenes in the decomposition into weight × level + jump of natural numbers. For natural numbers, the weight is the smallest prime factor of (n-1) and the level is the largest proper divisor of (n-1). Natural numbers classified by level are the (primes + 1) and natural numbers classified by weight are the (composites +1).
For prime numbers, this decomposition led to a new classification of primes. Primes classified by weight follow Legendre conjecture and i conjecture that primes classified by level rarefy. I think this conjecture is very important for the distribution of primes. It's easy to see and prove that lesser of twin primes (>3) have a weight of 3. So the twin primes conjecture can be rewritten: there are infinitely many primes that have a weight of 3.
I am not mathematician so i decompose sequences to promote my vision of numbers. By doing this decompositions, i apply a kind of sieve on each sequences. In some way, i find composites and primes of each sequences.