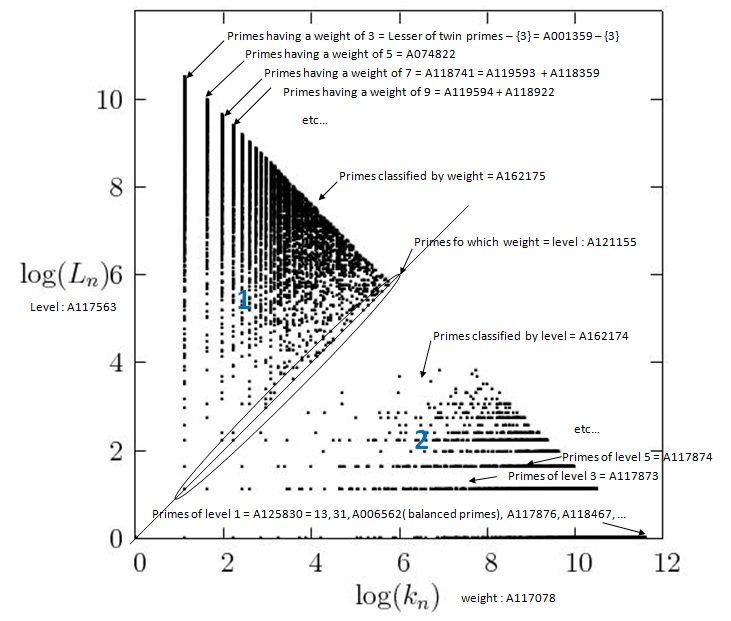
Decomposition into weight × level + jump of prime numbers commented - classification of prime numbers
2 trivialities:
- lesser of twin primes (except 3) have a weight of 3.
- by definition primes classified by weight (A162175) follow Legendre's conjecture and Andrica's conjecture.
- primes classified by level (A162174) are rarefying among prime numbers.
2, 3 and 7 are not classfied.
Zone 1: primes for which k(n) ≤ L(n) or primes classified by weight. We have the following relation:
- g(n) + 1 ≤ k(n) ≤ sqrt(l(n)) ≤ L(n) ≤ l(n) / 3
Zone 2: primes for which k(n) > L(n) or primes classified by level. We have the following relations:
- L(n) < sqrt(l(n)) < k(n) ≤ l(n)
- L(n) + 2 ≤ g(n) + 1 ≤ k(n) ≤ l(n)