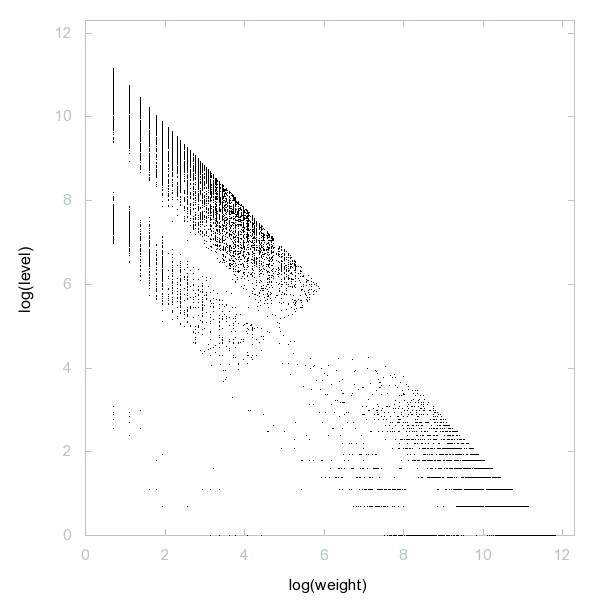
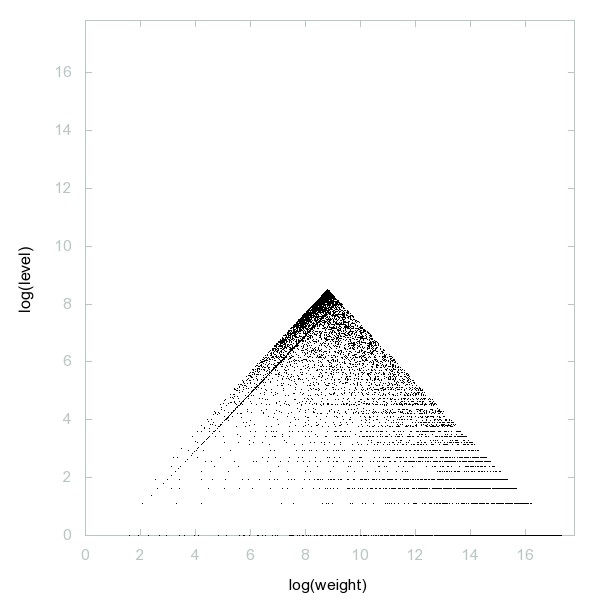
Decomposition of A095953
Initial values for f(x) = phi(sigma(x)) such that iteration of f ends in a cycle of length 3.
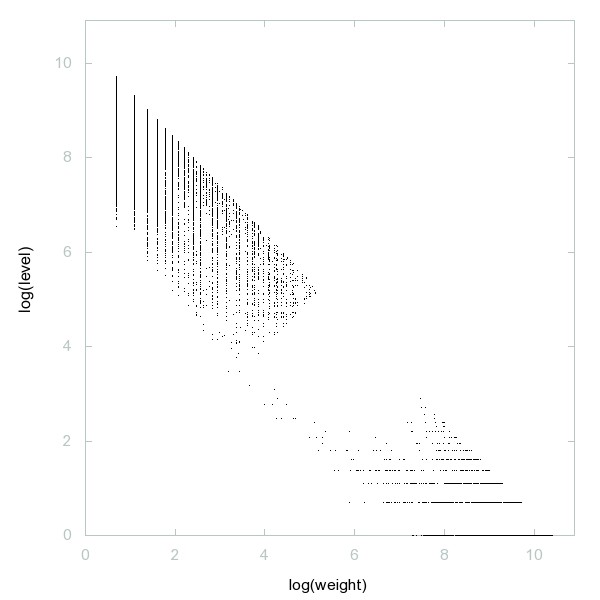
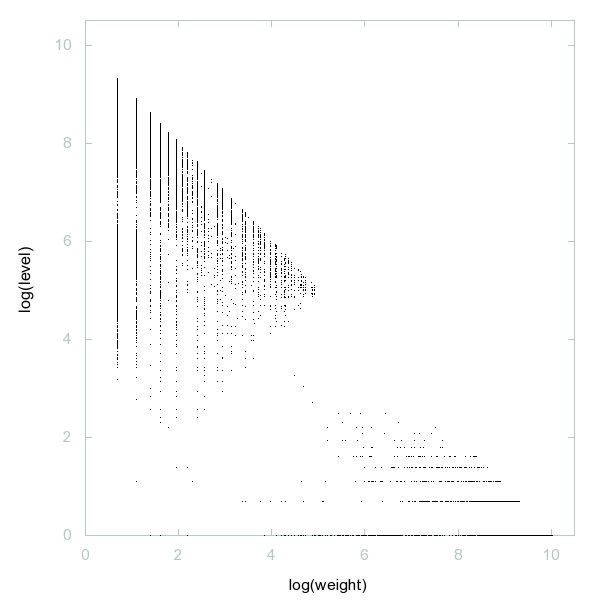
Decomposition of A095954
Initial values for f(x)=phi(sigma(x)) such that iteration of f ends in a cycle of length 6.
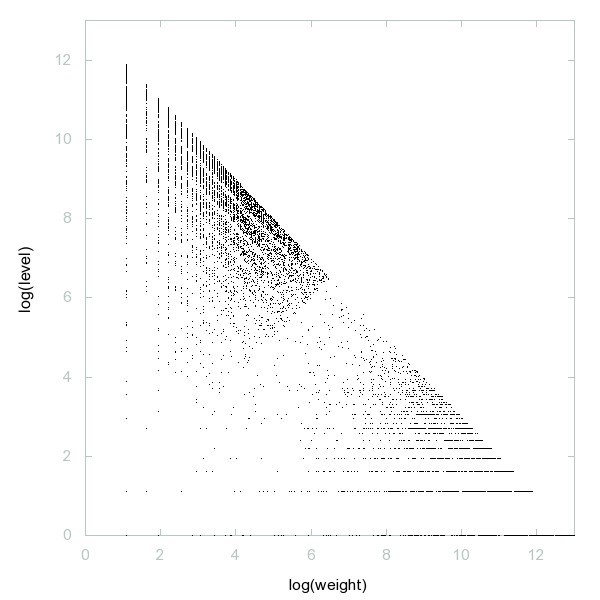
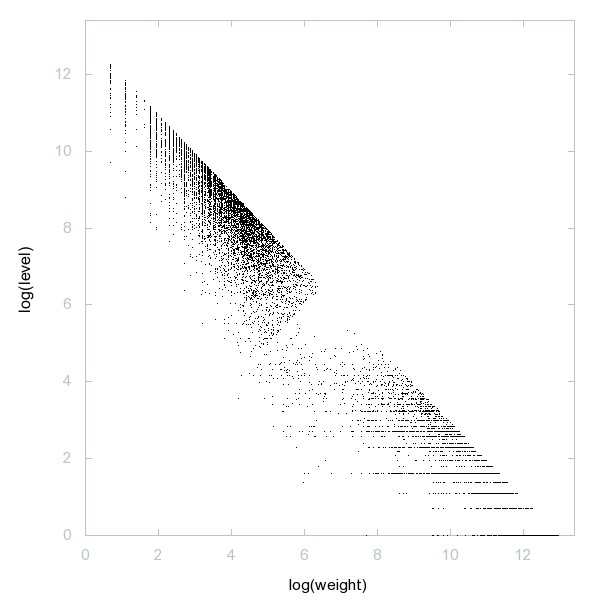
Decomposition of A096246
Base-2 deletable primes (written in base 10).
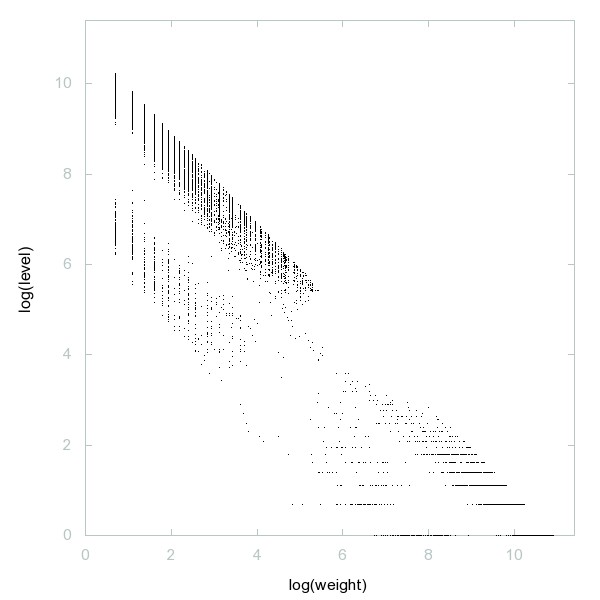
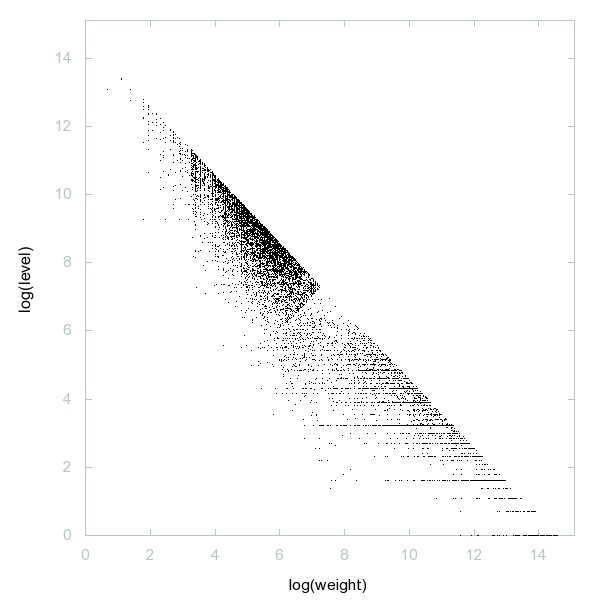
Decomposition of A096526
Initial values for f(x)=phi(sigma(x)) such that iteration of f ends in a cycle of length 4.
Decomposition of A096777
a(n) = a(n-1) + Sum_{k=1..n-1}(a(k) mod 2), a(1) = 1.
Decomposition of A096887
Initial values for f(x)=phi(sigma(x)) such that iteration of f ends in cycle of length=2.
Decomposition of A097102
Numbers n that are the hypotenuse of exactly 13 distinct integer sided right triangles, i.e. n^2 can be written as a sum of two squares in 13 ways.
Decomposition of A097103
Numbers n that are the hypotenuse of exactly 22 distinct integer sided right triangles, i.e. n^2 can be written as a sum of two squares in 22 ways.
Decomposition of A097752
Least integer with each "mod 4 prime signature".
Decomposition of A097933
Primes such that p divides 3^((p-1)/2) - 1.