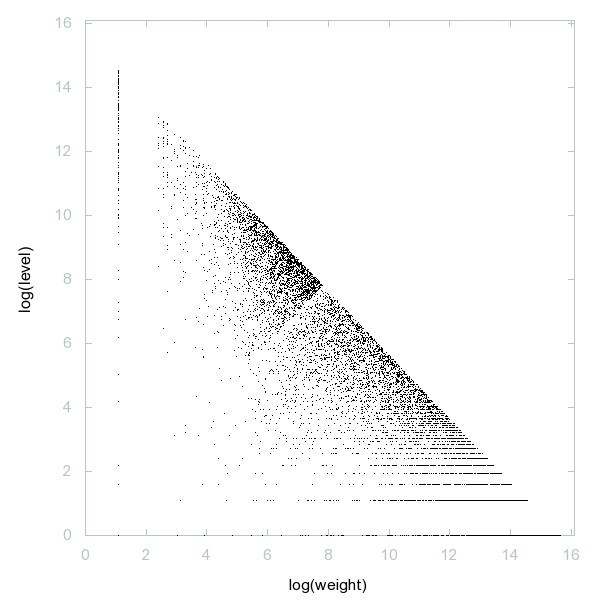
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of A209203

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Values of the difference d for 4 primes in geometric-arithmetic progression with the minimal sequence {5*5^j + j*d}, j = 0 to 3.
A209203(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A209203 (9999 lines.)
Decomposition of A209203 - 9996 dots.

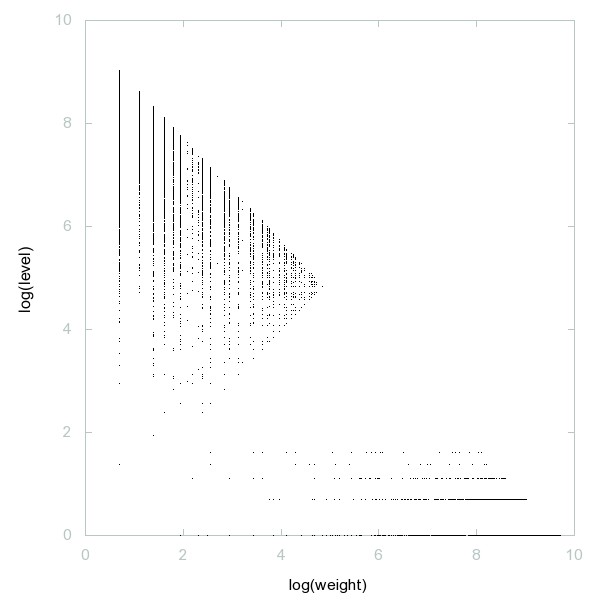
Decomposition of A210479

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes p with p-1 and p+1 both practical: "Sandwich of the first kind".
A210479(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A210479 (9999 lines.)
Decomposition of A210479 - 9994 dots.

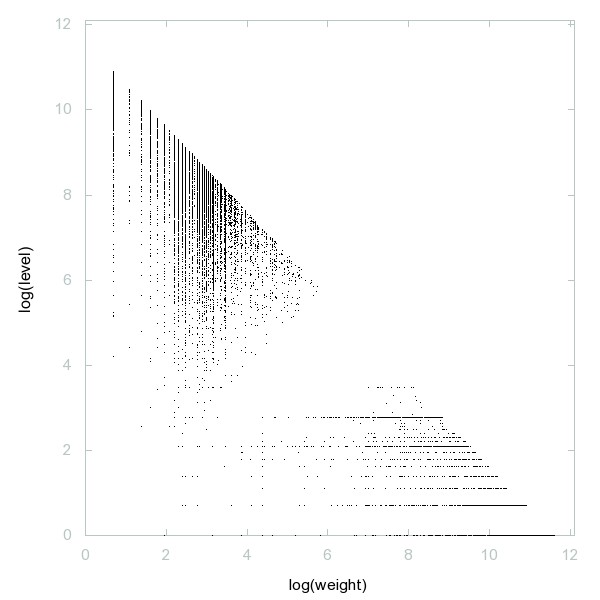
Decomposition of A211223

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n for which sigma(n) = sigma(x) + sigma(y), where n = x + y.
A211223(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A211223 (9999 lines.)
Decomposition of A211223 - 9997 dots.

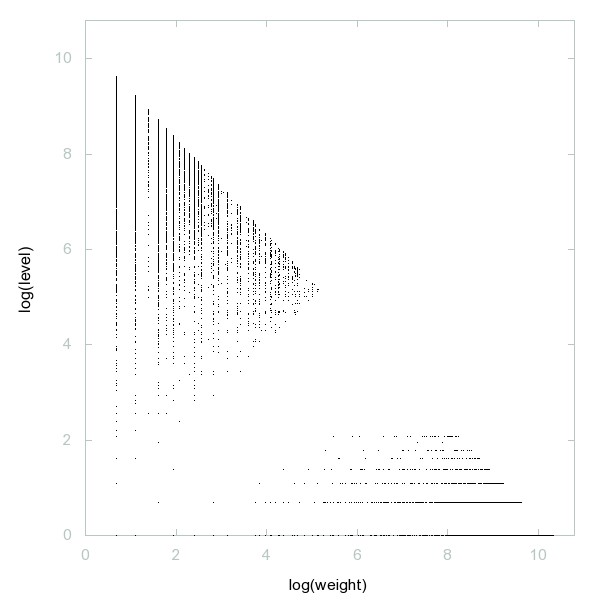
Decomposition of A212164

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that the maximal exponent in its prime factorization is greater than the number of positive exponents (A051903(n) > A001221(n)).
A212164(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A212164 (9999 lines.)
Decomposition of A212164 - 9996 dots.

Decomposition of A212165

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that the maximal exponent in its prime factorization is not less than the number of positive exponents (A051903(n) >= A001221(n)).
A212165(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A212165 (9999 lines.)
Decomposition of A212165 - 9997 dots.

Decomposition of A212166

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that the maximal exponent in its prime factorization equals the number of positive exponents (A051903(n) = A001221(n)).
A212166(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A212166 (9999 lines.)
Decomposition of A212166 - 9995 dots.

Decomposition of A212168

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that the maximal exponent in its prime factorization is less than the number of positive exponents (A051903(n) < A001221(n)).
A212168(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A212168 (9999 lines.)
Decomposition of A212168 - 9998 dots.

Decomposition of A213382

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that n^n mod (n + 2) = n.
A213382(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A213382 (9999 lines.)
Decomposition of A213382 - 9995 dots.

Decomposition of A214423

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n palindromic in only one base b, 2 <= b <= 10.
A214423(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A214423 (9999 lines.)
Decomposition of A214423 - 9998 dots.

Decomposition of A215940

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Difference between the n-th and the first (identity) permutation of (1,...,m), interpreted as a decimal number, divided by 9 (for any m for which m! >= n).
A215940(n) = A000000(n) * A000000(n) + A217626(n)
Download CSV of the decomposition of A215940 (9999 lines.)
Decomposition of A215940 - 9991 dots.