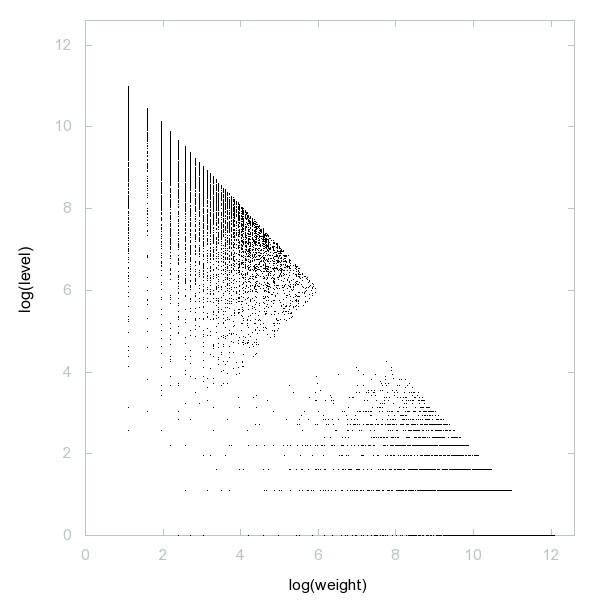
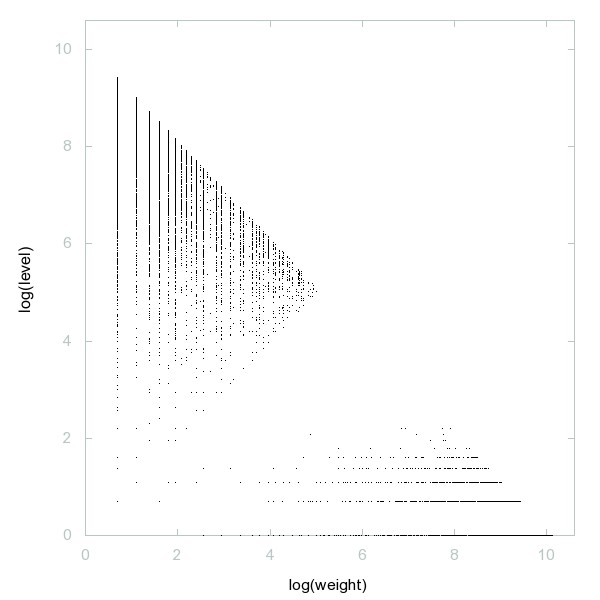
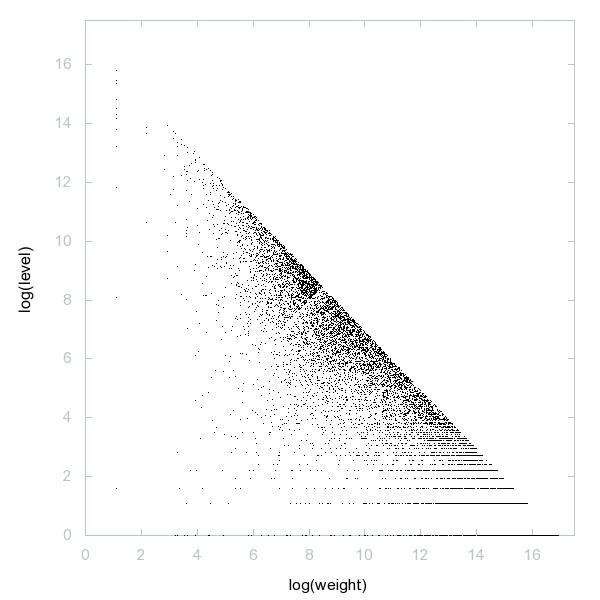
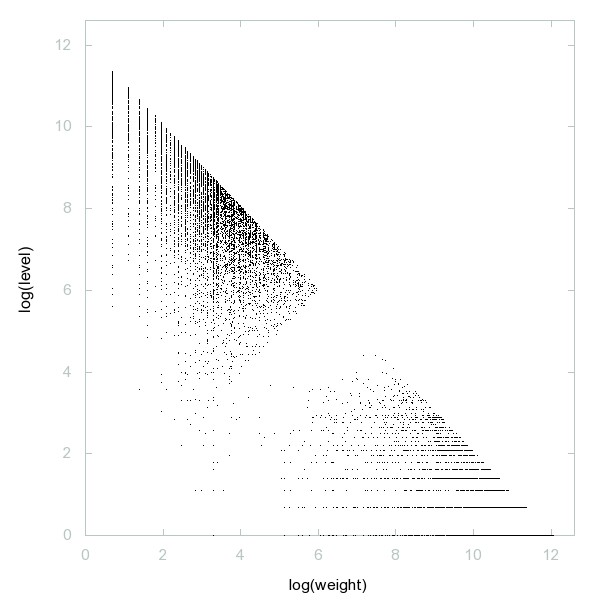
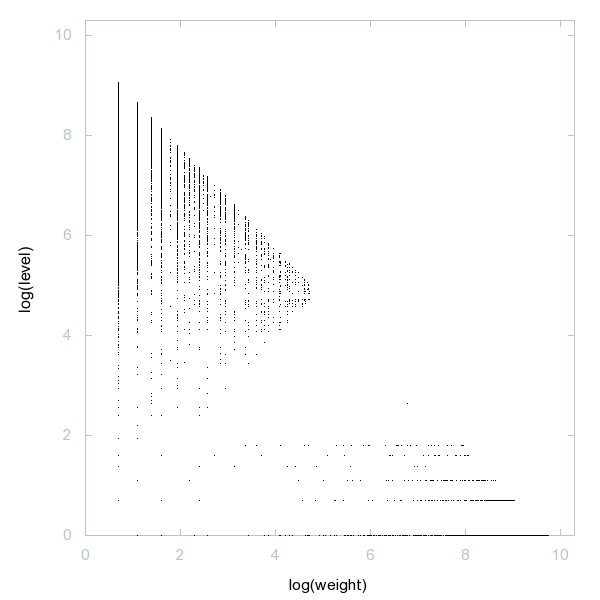
Decomposition of A216838
Odd primes for which 2 is not a primitive root.
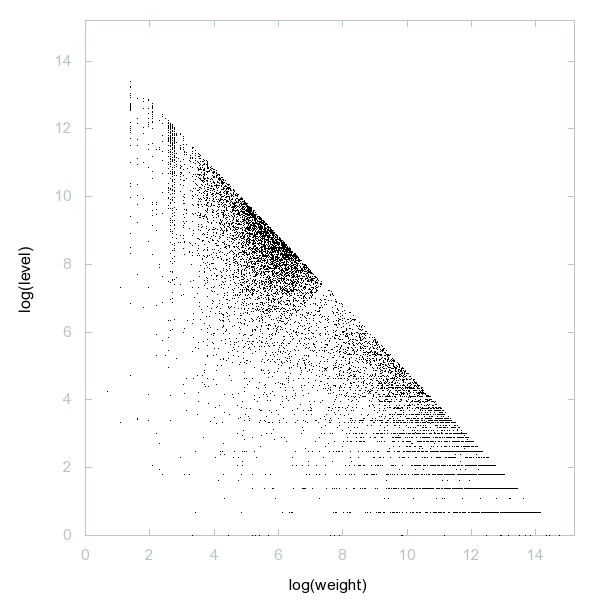
Decomposition of A217139
Numbers n such that phi(n) = phi(n+12), with Euler's totient function phi = A000010.
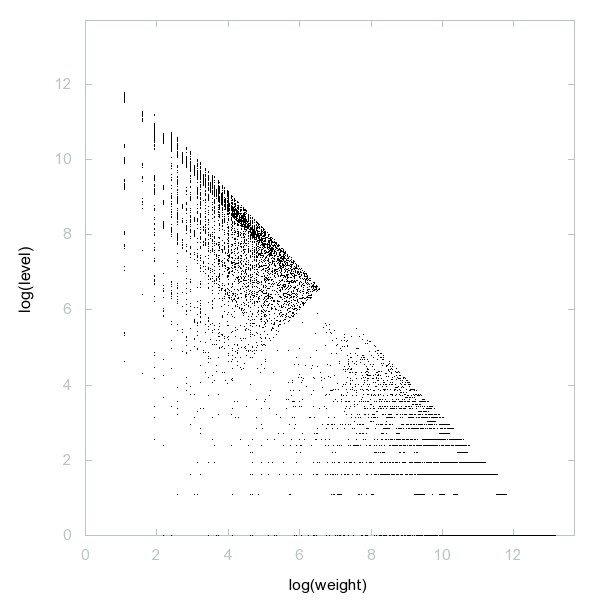
Decomposition of A227916
Primes that remain prime when the leftmost digit is removed.
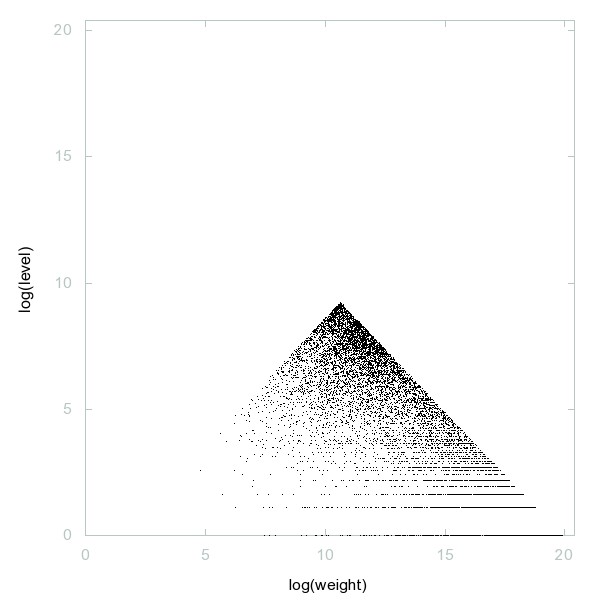
Decomposition of A228183
Semiprimes generated by the Euler polynomial x^2 + x + 41.
Decomposition of A230044
Nonnegative numbers n such that n plus a perfect square is a triangular number.
Decomposition of A230091
Numbers of the form k + wt(k) for exactly two distinct k, where wt(k) = A000120(k) is the binary weight of k.
Decomposition of A230092
Numbers of the form k + wt(k) for exactly three distinct k, where wt(k) = A000120(k) is the binary weight of k.
Decomposition of A230223
Primes p such that 3*p-4, 3*p-10, and 3*p-14 are all prime.
Decomposition of A230577
Positive integers that have exactly 6 odd divisors.
Decomposition of A230633
Numbers n such that m + (sum of digits in base-4 representation of m) = n has exactly one solution.