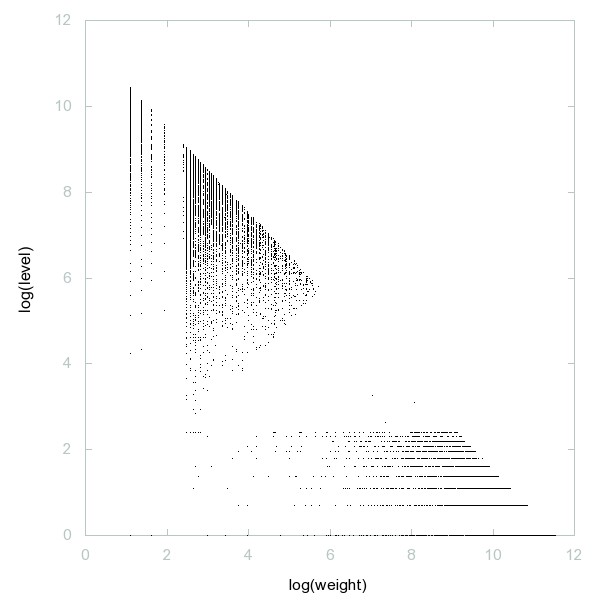
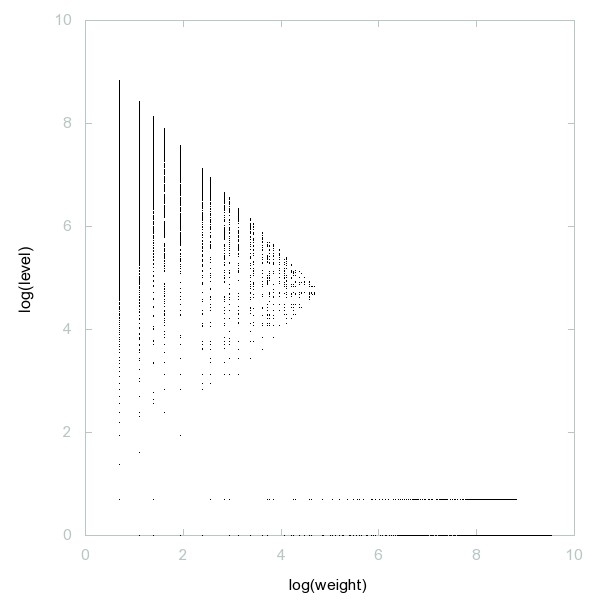
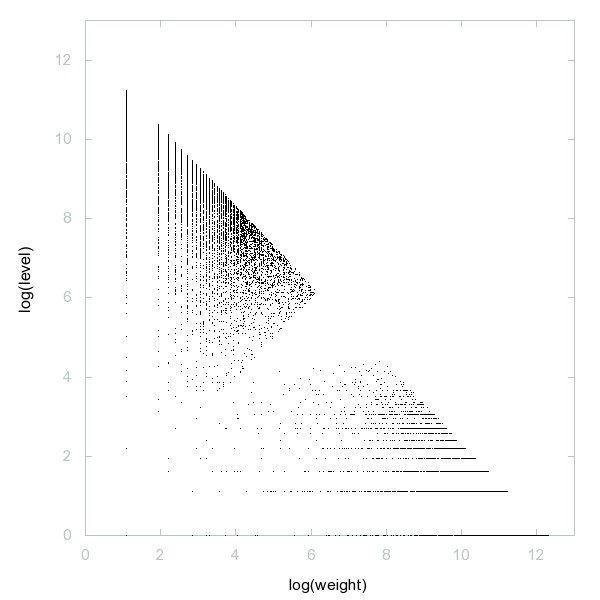
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of Self numbers

3D graph (WebGL) / 2D graph - First 500 terms
Self or Colombian numbers (not of form n + sum of digits of n).
A003052(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of Self numbers (9999 lines.)
Decomposition of Self numbers - 9995 dots.

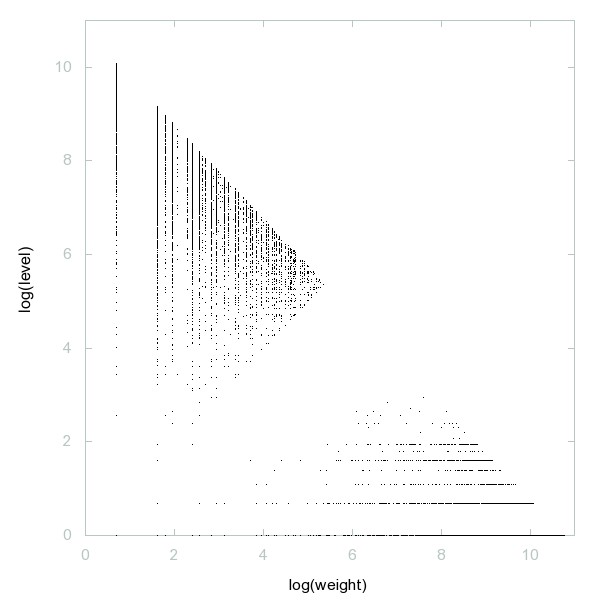
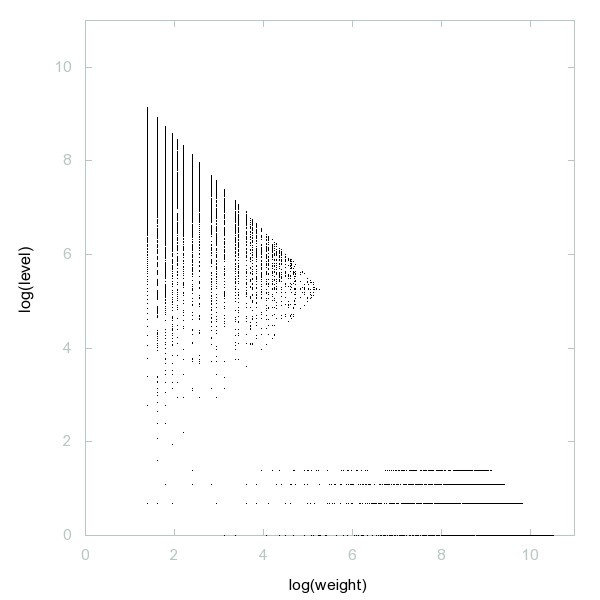
Decomposition of Loeschian numbers

3D graph (WebGL) / 2D graph - First 500 terms
Loeschian numbers: numbers of the form x^2 + xy + y^2; norms of vectors in A2 lattice.
A003136(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of Loeschian numbers (9999 lines.)
Decomposition of Loeschian numbers - 9996 dots.

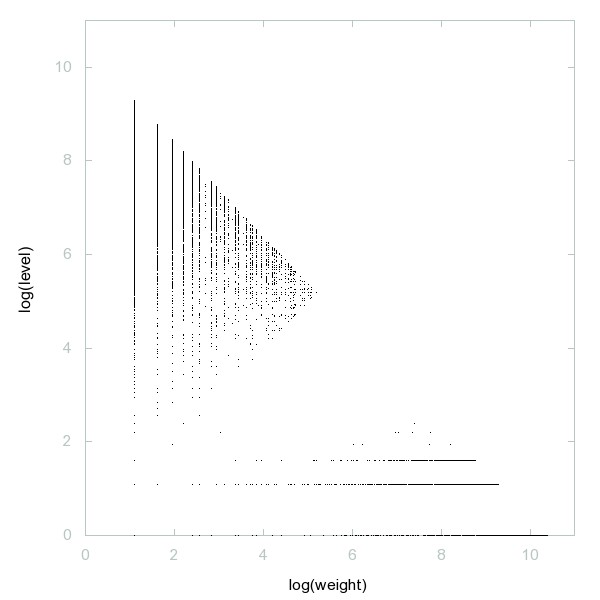
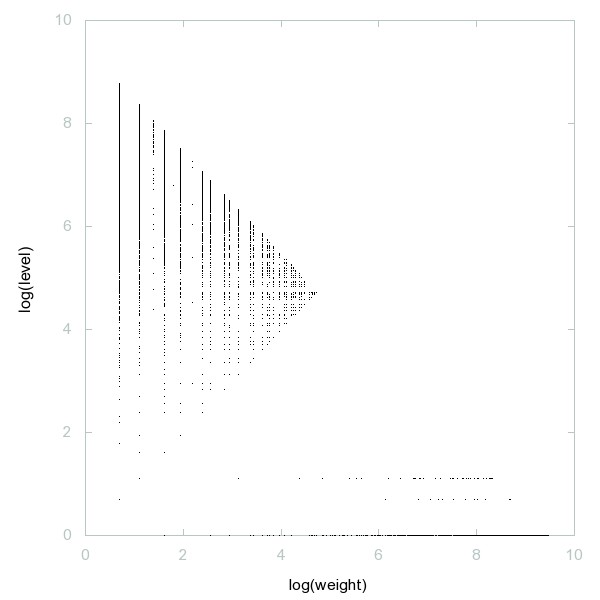
Decomposition of Cyclic numbers

3D graph (WebGL) / 2D graph - First 500 terms
Cyclic numbers: n such that n and phi(n) are relatively prime; also n such that there is just one group of order n, i.e. A000001(n) = 1.
A003277(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of Cyclic numbers (9999 lines.)
Decomposition of Cyclic numbers - 9995 dots.

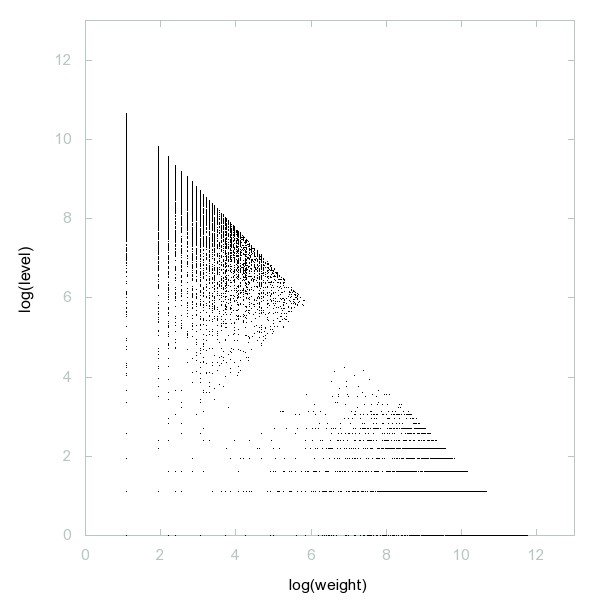
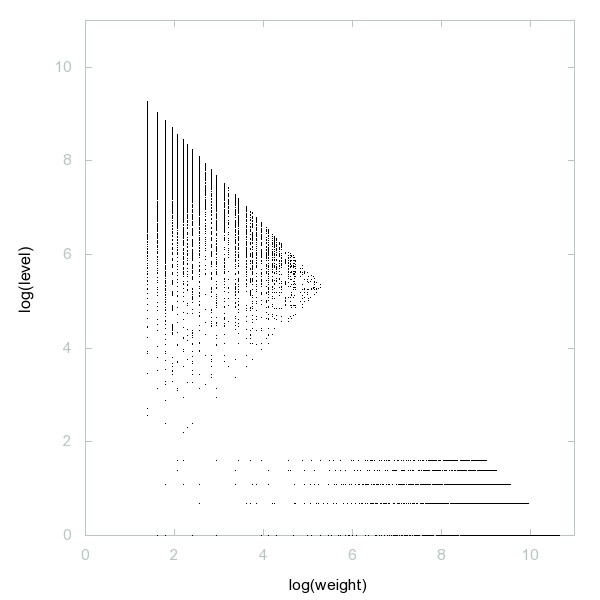
Decomposition of Ludic numbers

3D graph (WebGL) / 2D graph - First 500 terms
Ludic numbers: apply the same sieve as Eratosthenes, but cross off every k-th /remaining/ number.
A003309(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of Ludic numbers (10000 lines.)
Decomposition of Ludic numbers - 9996 dots.

Decomposition of A003485

3D graph (WebGL) / 2D graph - First 500 terms
Hurwitz-Radon function at powers of 2.
A003485(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A003485 (10000 lines.)
Decomposition of A003485 - 9997 dots.

Decomposition of A003511

3D graph (WebGL) / 2D graph - First 500 terms
A Beatty sequence: floor( n * (1 + sqrt(3))/2 ).
A003511(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A003511 (9999 lines.)
Decomposition of A003511 - 9997 dots.

Decomposition of A003512

3D graph (WebGL) / 2D graph - First 500 terms
A Beatty sequence: floor(n*(sqrt(3) + 2)).
A003512(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A003512 (9999 lines.)
Decomposition of A003512 - 9997 dots.

Decomposition of A003601

3D graph (WebGL) / 2D graph - First 500 terms
Numbers n such that the average of the divisors of n is an integer: sigma_0(n) divides sigma_1(n). Alternatively, tau(n) (A000005(n)) divides sigma(n) (A000203(n)).
A003601(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A003601 (9999 lines.)
Decomposition of A003601 - 9996 dots.

Decomposition of A003623

3D graph (WebGL) / 2D graph - First 500 terms
From a 3-way splitting of positive integers: [[n*phi^2]*phi].
A003623(n) = A000000(n) * A000000(n) + A194584(n)
Download CSV of the decomposition of A003623 (9999 lines.)
Decomposition of A003623 - 9998 dots.

Decomposition of A003628

3D graph (WebGL) / 2D graph - First 500 terms
Primes congruent to {5, 7} mod 8.
A003628(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A003628 (9999 lines.)
Decomposition of A003628 - 9997 dots.