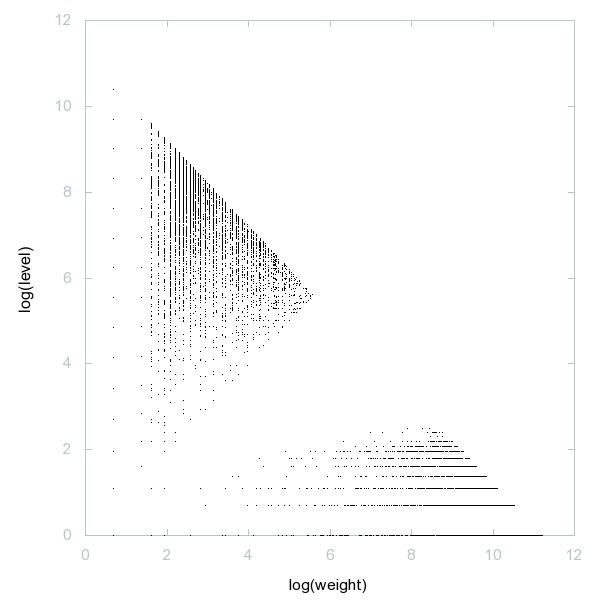
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of A176995

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers that can be written as (m + sum of digits of m) for some m.
A176995(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A176995 (9999 lines.)
Decomposition of A176995 - 9997 dots.

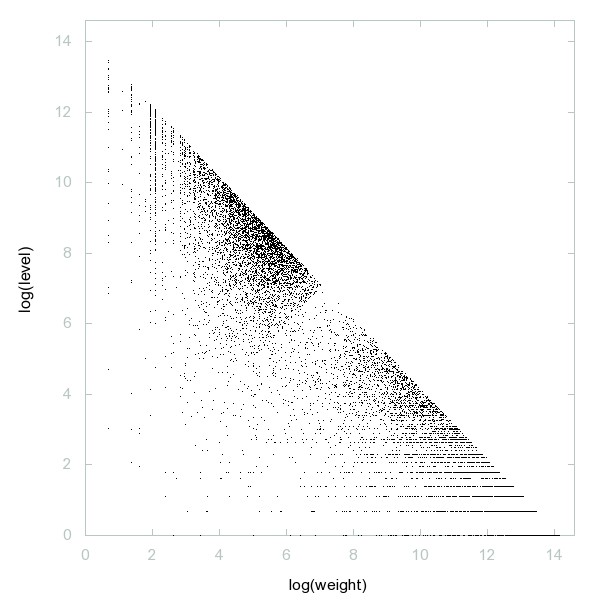
Decomposition of A177729

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Positive integers which do not appear in a Collatz sequence starting from a smaller positive integer.
A177729(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A177729 (9999 lines.)
Decomposition of A177729 - 9996 dots.

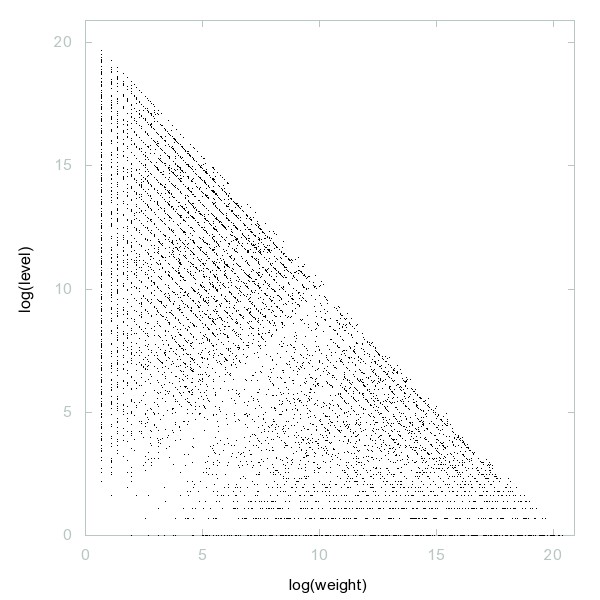
Decomposition of A178361

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers with rounded up arithmetic mean of digits = 1.
A178361(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A178361 (9999 lines.)
Decomposition of A178361 - 9990 dots.

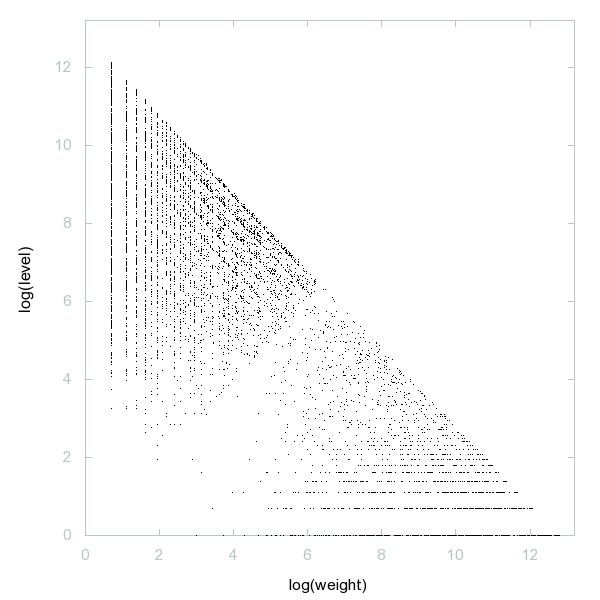
Decomposition of A178403

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers containing the rounded up arithmetic mean of their digits at least once, cf. A004427.
A178403(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A178403 (9999 lines.)
Decomposition of A178403 - 9995 dots.

Decomposition of A179016

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
The only infinite sequence such that a(n-1) = a(n) - number of 1's in binary representation of a(n).
A179016(n) = A000000(n) * A000000(n) + A213712(n)
Download CSV of the decomposition of A179016 (10000 lines.)
Decomposition of A179016 - 9997 dots.

Decomposition of A179186

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that phi(n) = phi(n+4), with Euler's totient function phi=A000010.
A179186(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A179186 (9999 lines.)
Decomposition of A179186 - 9995 dots.

Decomposition of A179188

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that phi(n) = phi(n+6), with Euler's totient function phi=A000010.
A179188(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A179188 (9999 lines.)
Decomposition of A179188 - 9999 dots.

Decomposition of A179243

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n that have three terms in their Zeckendorf representation.
A179243(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A179243 (9999 lines.)
Decomposition of A179243 - 9999 dots.

Decomposition of A179244

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n that have 4 terms in their Zeckendorf representation.
A179244(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A179244 (9999 lines.)
Decomposition of A179244 - 9999 dots.

Decomposition of A179336

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes containing at least one prime digit in base 10.
A179336(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A179336 (9999 lines.)
Decomposition of A179336 - 9996 dots.