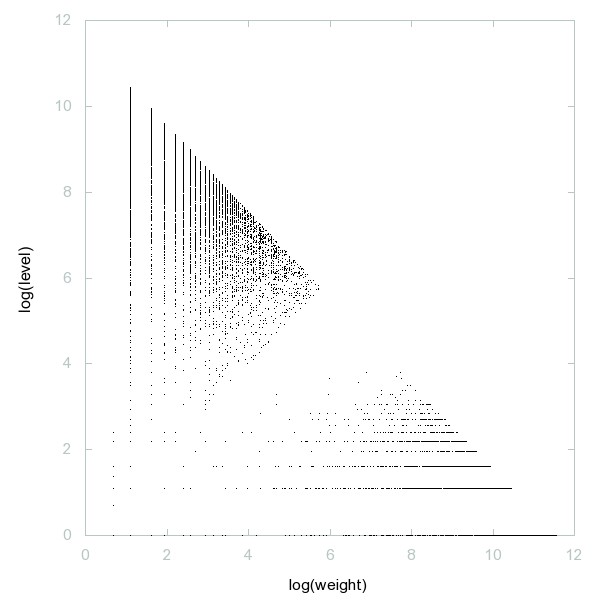
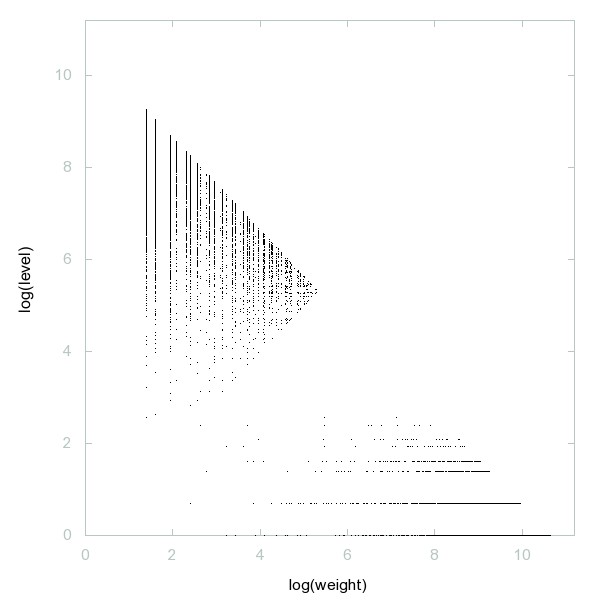
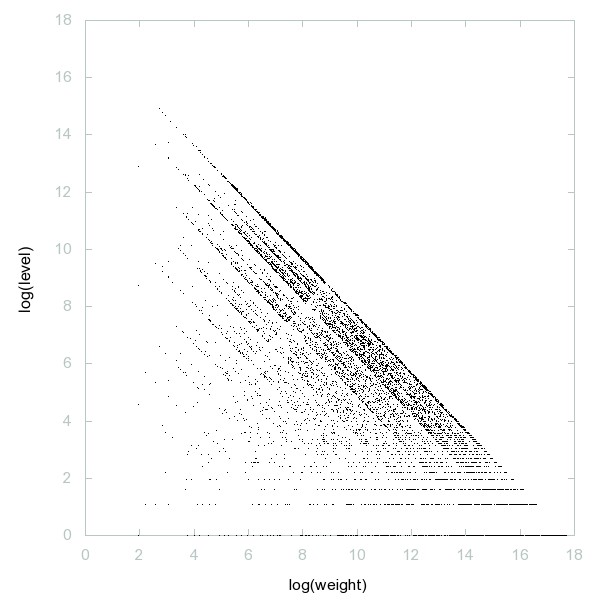
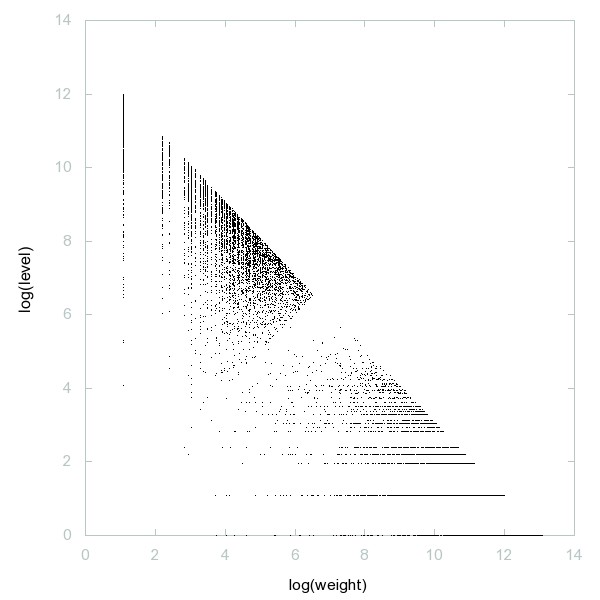
Decomposition of Binomial primes
Binomial primes: positive integers n such that every i not coprime to n and not exceeding n/2 does not divide binomial(n-i-1,i-1).
Decomposition of A138511
Semiprimes where the larger prime factor is greater than the square of the smaller prime factor, short: semiprimes p*q, p^2 < q.
Decomposition of A138685
Numbers n such that there is no prime of the form 2n + p^2 for any prime p.
Decomposition of Toothpicks
Toothpick sequence.
Decomposition of A141111
Primes of the form 4*x^2+x*y-4*y^2 (as well as of the form 4*x^2+9*x*y+y^2).
Decomposition of A141112
Primes of the form 2*x^2+5*x*y-5*y^2 (as well as of the form 7*x^2+11*x*y+2*y^2).
Decomposition of A141161
Primes of the form 4*x^2+6*x*y-7*y^2.
Decomposition of A141165
Primes of the form 9*x^2+7*x*y-5*y^2.
Decomposition of A141183
Primes of the form -x^2+6*x*y+2*y^2 (as well as of the form 7*x^2+10*x*y+2*y^2).
Decomposition of A141301
Primes of the form x^2+6*x*y-6*y^2 (as well as of the form x^2+8*x*y+y^2).