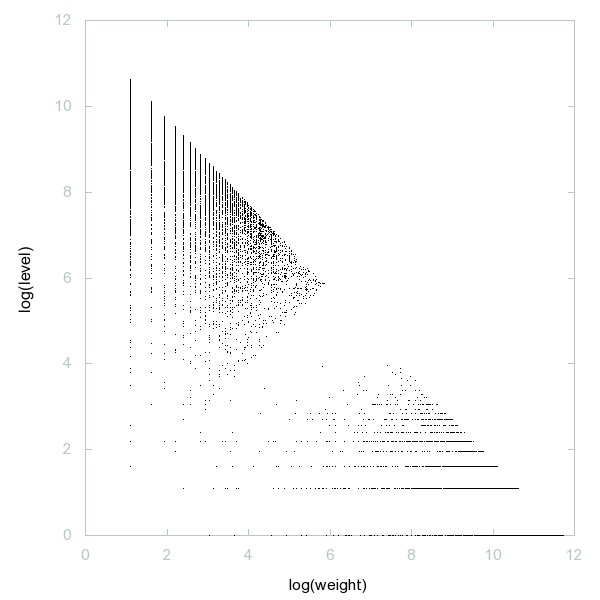
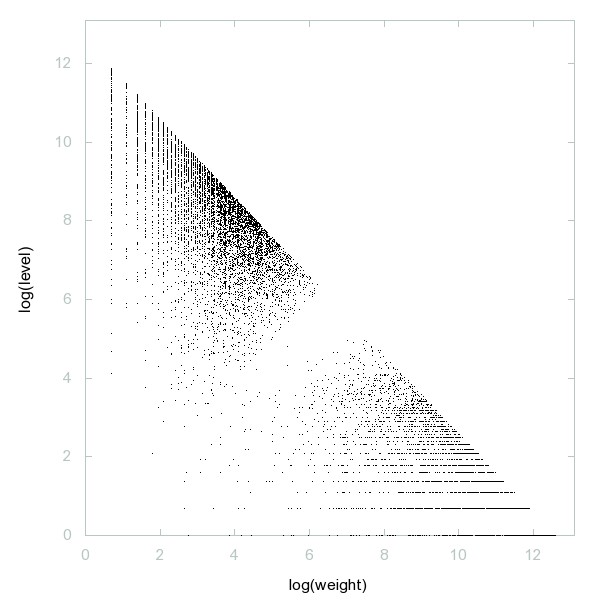
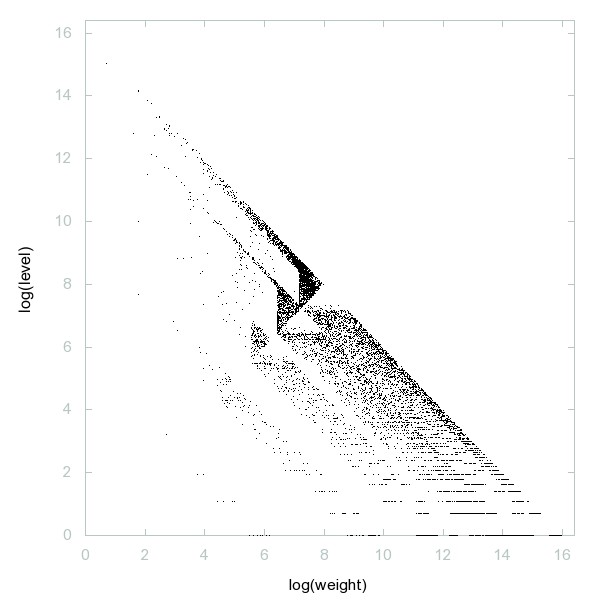
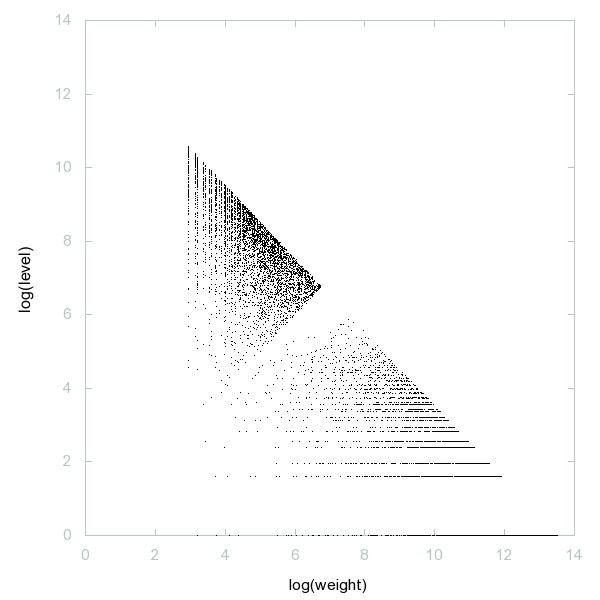
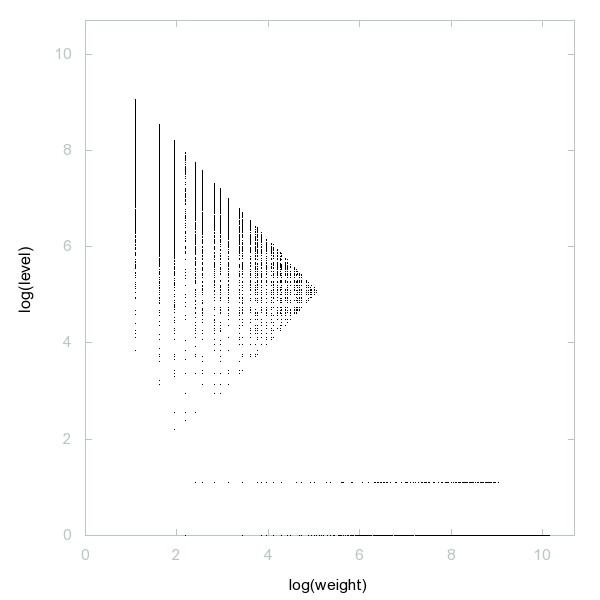
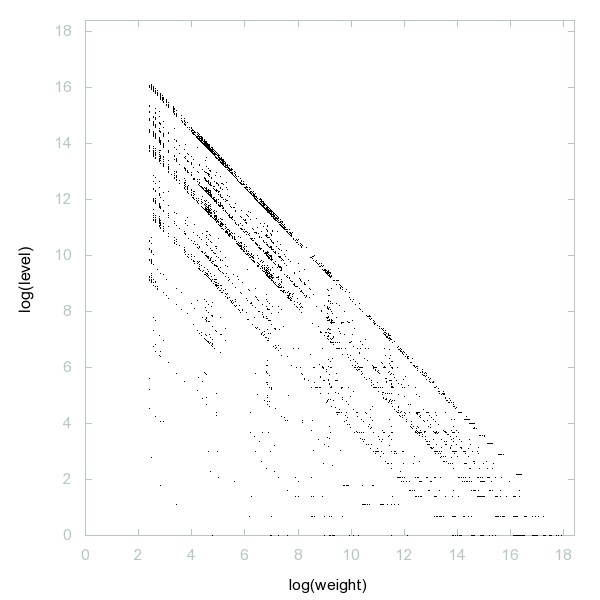
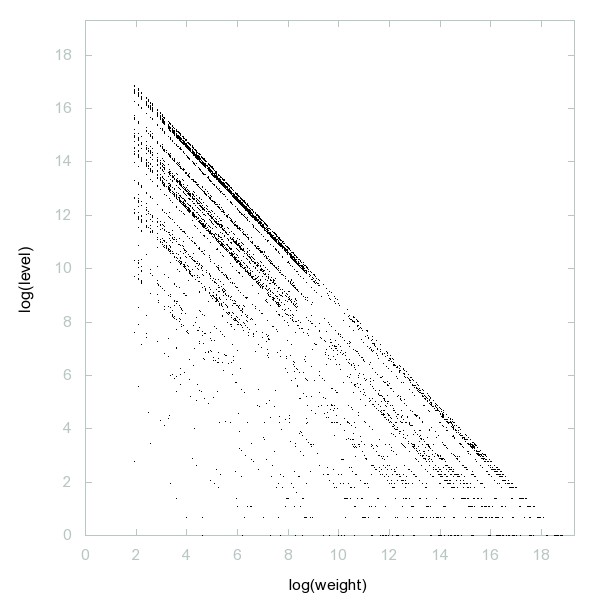
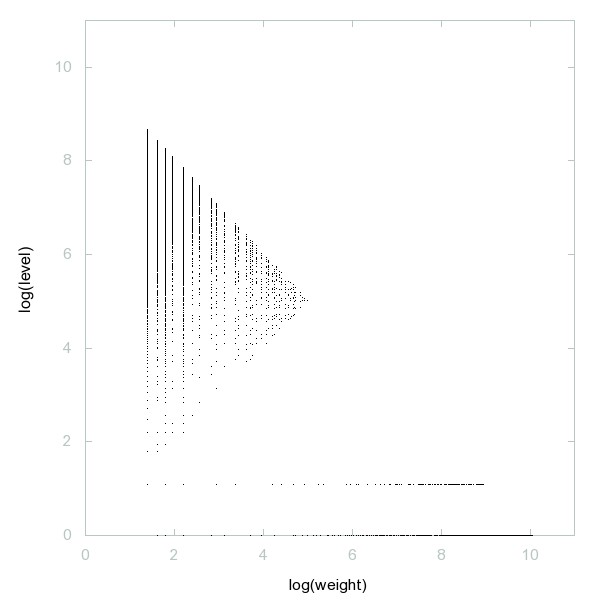
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of A060254

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes which are the sum of two consecutive composite numbers.
A060254(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A060254 (9999 lines.)
Decomposition of A060254 - 9998 dots.

Decomposition of A060874

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Intrinsic 4-palindromes: n is an intrinsic k-palindrome if it is a k-digit palindrome in some base.
A060874(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A060874 (9999 lines.)
Decomposition of A060874 - 9997 dots.

Decomposition of A060879

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Intrinsic 9-palindromes: n is an intrinsic k-palindrome if it is a k-digit palindrome in some base.
A060879(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A060879 (9999 lines.)
Decomposition of A060879 - 9997 dots.

Decomposition of A060947

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Intrinsic 10-palindromes: n is an intrinsic k-palindrome if it is a k-digit palindrome in some base.
A060947(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A060947 (9999 lines.)
Decomposition of A060947 - 9996 dots.

Decomposition of A061241

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Prime numbers == 7 (mod 9).
A061241(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A061241 (9999 lines.)
Decomposition of A061241 - 9997 dots.

Decomposition of A061276

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers which are sums of repdigits of their digits.
A061276(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A061276 (7473 lines.)
Decomposition of A061276 - 7468 dots.

Decomposition of A061346

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Odd numbers that are neither primes nor prime powers.
A061346(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A061346 (9999 lines.)
Decomposition of A061346 - 9998 dots.

Decomposition of A061384

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n with property that sum of digits = number of digits.
A061384(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A061384 (9999 lines.)
Decomposition of A061384 - 9990 dots.

Decomposition of A061426

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Geometric mean of the digits = 2. In other words the product of the digits is = 2^k where k is the number of digits.
A061426(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A061426 (9999 lines.)
Decomposition of A061426 - 9988 dots.

Decomposition of A061641

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Pure numbers in the Collatz (3x+1) iteration. Also called pure hailstone numbers.
A061641(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A061641 (9999 lines.)
Decomposition of A061641 - 9996 dots.