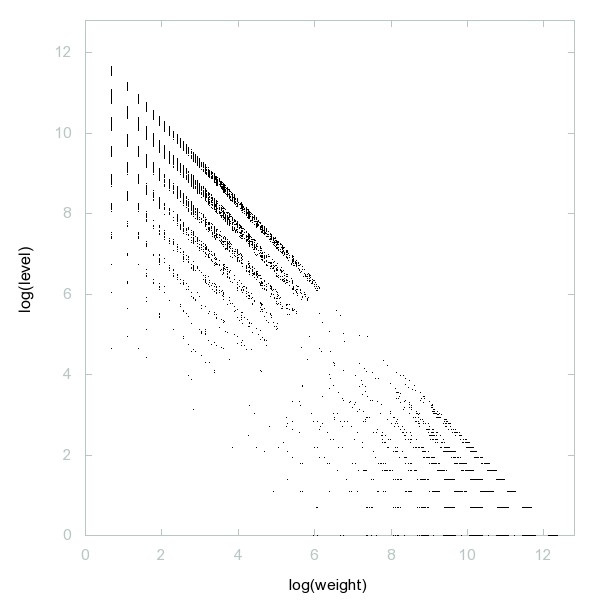
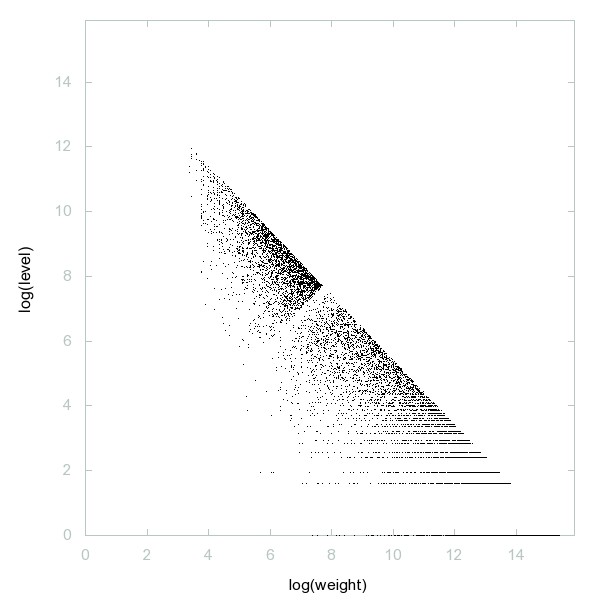
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of A061656

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
In base 2 n and n^2 contain the same digits in the same proportion.
A061656(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A061656 (9999 lines.)
Decomposition of A061656 - 9993 dots.

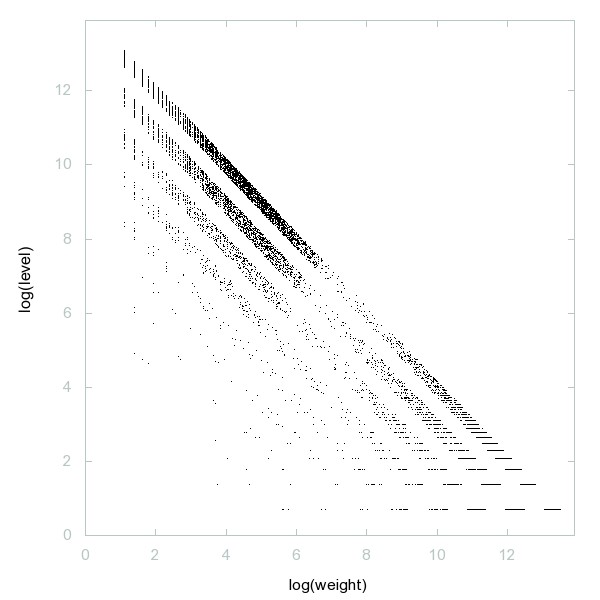
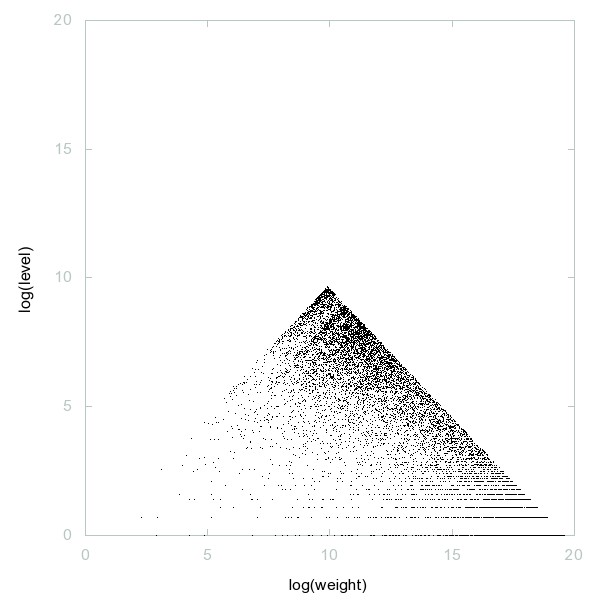
Decomposition of A061657

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
In base 3 n and n^2 contain the same digits in the same proportion.
A061657(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A061657 (9999 lines.)
Decomposition of A061657 - 9991 dots.

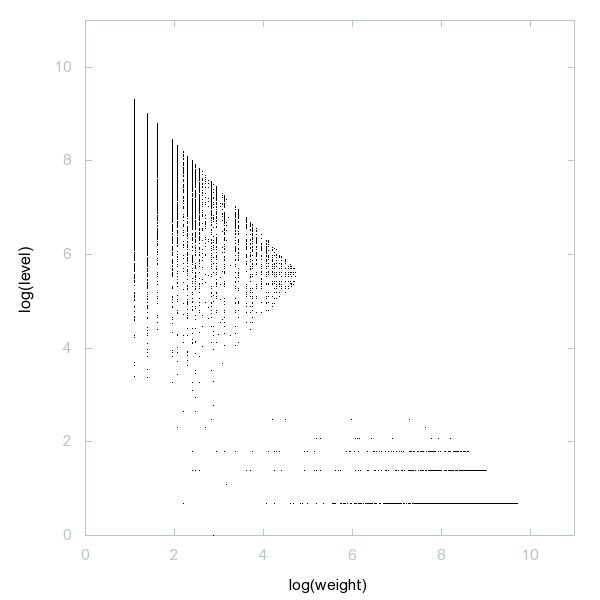
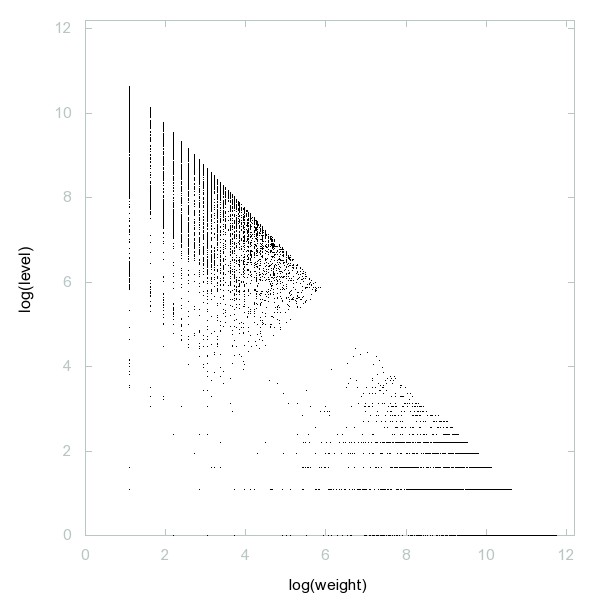
Decomposition of A061673

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Even numbers n such that n+1 and n-1 are both composite.
A061673(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A061673 (10000 lines.)
Decomposition of A061673 - 10000 dots.

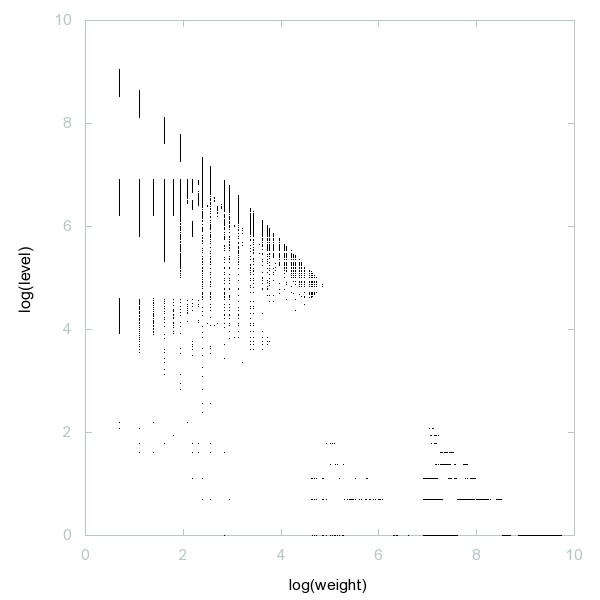
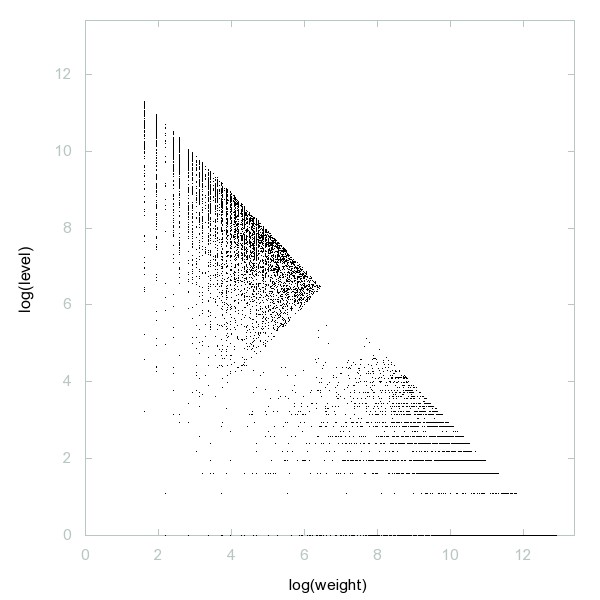
Decomposition of A061681

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
a(0)=1; a(n)=a(n-1)+lead(a(n-1)) for n > 0 where for an integer x lead(x) is the leading digit in base 10.
A061681(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A061681 (9999 lines.)
Decomposition of A061681 - 9996 dots.

Decomposition of A061779

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes p such that q-p = 22, where q is the next prime after p.
A061779(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A061779 (9999 lines.)
Decomposition of A061779 - 9998 dots.

Decomposition of A061812

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that floor(Pi*n) is a square.
A061812(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A061812 (10000 lines.)
Decomposition of A061812 - 9995 dots.

Decomposition of A062060

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers with 10 odd integers in their Collatz (or 3x+1) trajectory.
A062060(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A062060 (9999 lines.)
Decomposition of A062060 - 9983 dots.

Decomposition of A062115

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers with no prime substring in their decimal expansion.
A062115(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A062115 (9999 lines.)
Decomposition of A062115 - 9991 dots.

Decomposition of A062634

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Every divisor contains the digit 1.
A062634(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A062634 (9999 lines.)
Decomposition of A062634 - 9997 dots.

Decomposition of A062721

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that n is a product of two primes and n-2 is prime.
A062721(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A062721 (9999 lines.)
Decomposition of A062721 - 9997 dots.