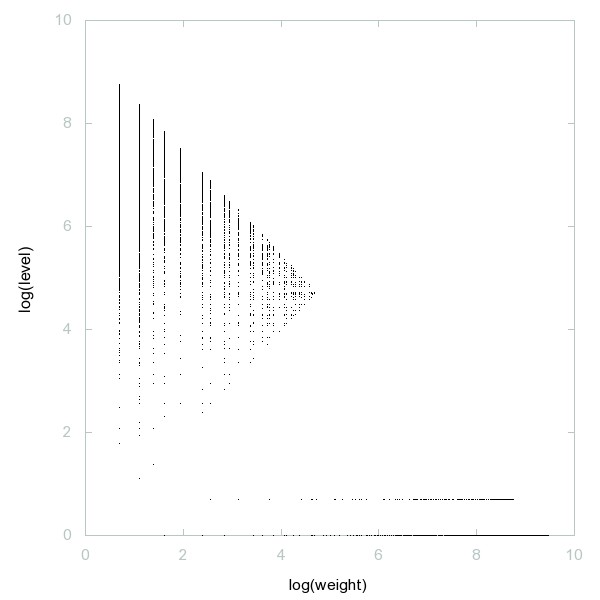
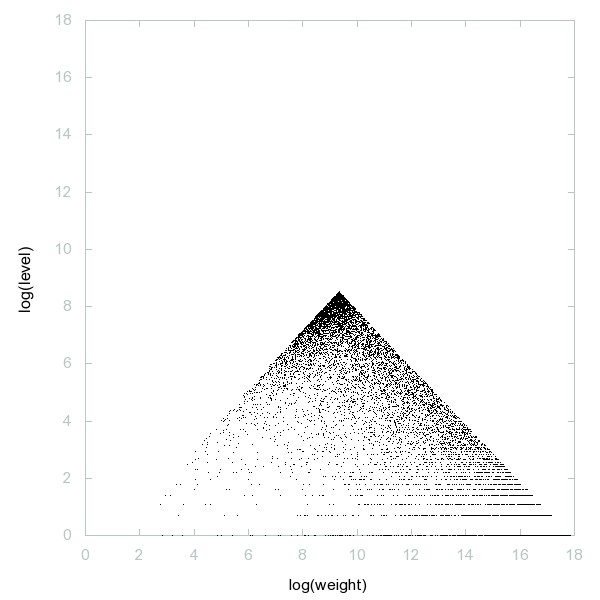
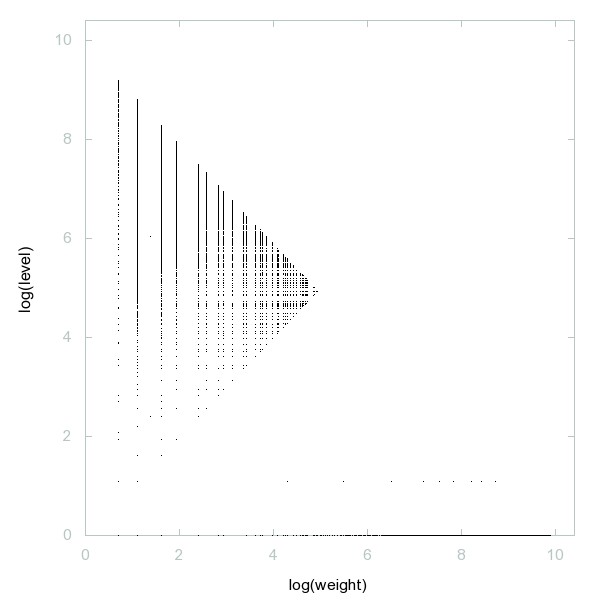
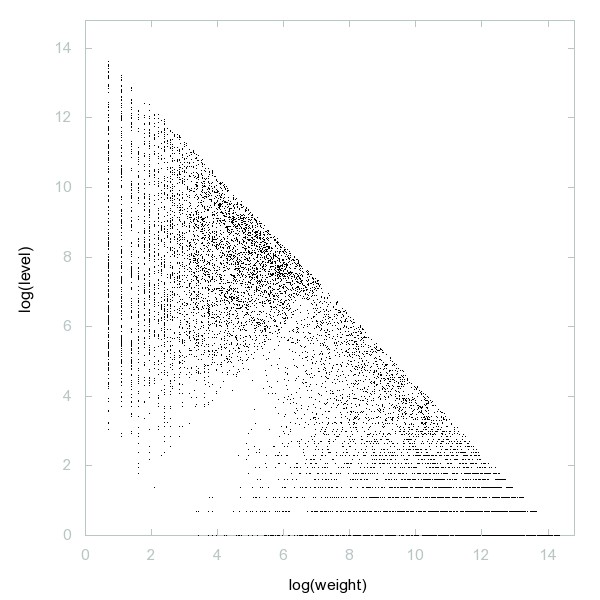
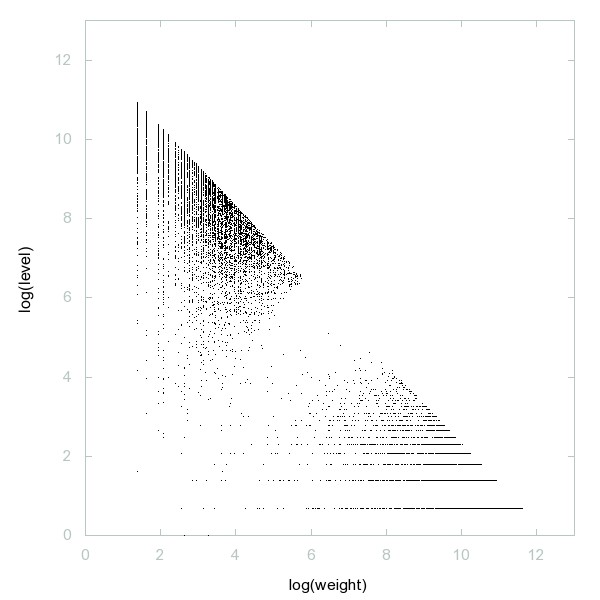
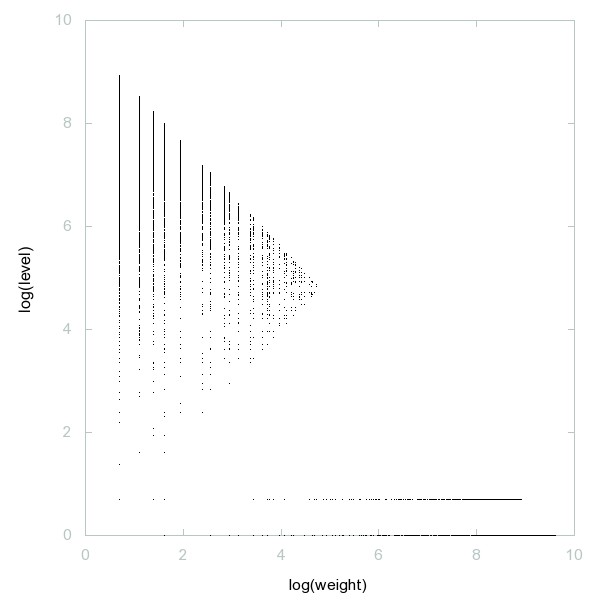
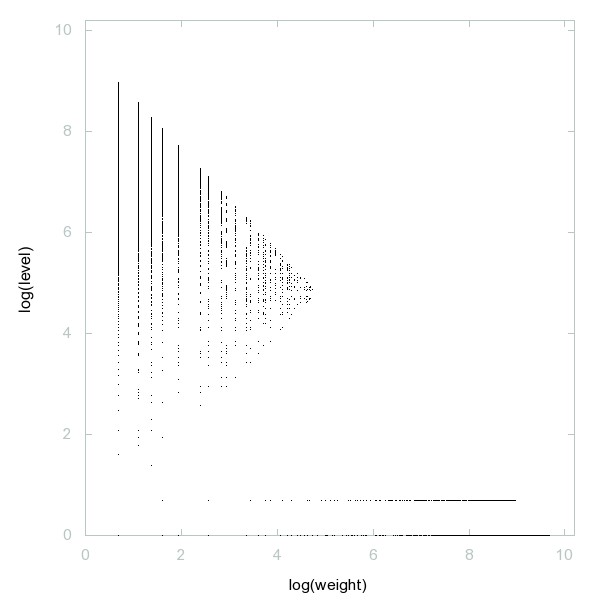
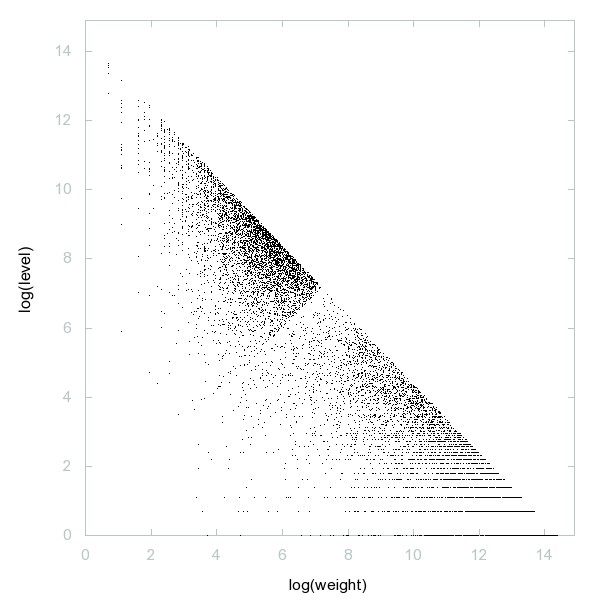
Decomposition of Flag numbers
"Flag numbers": number of dots that can be arranged in successive rows of K, K-1, K, K-1, K, ..., K-1, K (assuming there is a total of L > 1 rows of size K > 1).
Decomposition of A053767
Sum of first n composite numbers.
Decomposition of A053868
Numbers n such that sum of divisors of n less than n is odd.
Decomposition of A054032
Numbers n such that n^2 contains exactly 4 different digits.
Decomposition of A054211
Numbers n such that n concatenated with n-1 is prime.
Decomposition of A054217
Primes p with property that p concatenated with its emirp p' (prime reversal) forms a palindromic prime of the form 'primemirp' (rightmost digit of p and leftmost digit of p' are blended together - p and p' palindromic allowed).
Decomposition of A054353
Partial sums of Kolakoski sequence A000002.
Decomposition of A054385
Beatty sequence for e/(e-1); complement of A022843.
Decomposition of A054402
Numbers that are the sum of a positive square and a positive cube in more than one way.
Decomposition of A054520
Let S = {1,5,9,13,..., 4n+1, ...} and call p in S an S-prime if p>1 and the only divisors of p in S are 1 and p; sequence gives elements of S that are not S-primes.