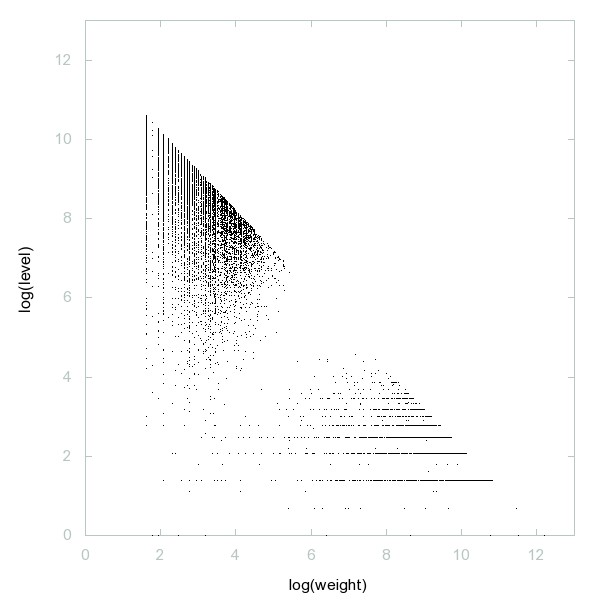
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of A033203

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes congruent to {1, 2, 3} mod 8; or primes of form x^2+2*y^2; or primes p such that x^2 = -2 has a solution mod p.
A033203(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A033203 (10000 lines.)
Decomposition of A033203 - 9996 dots.

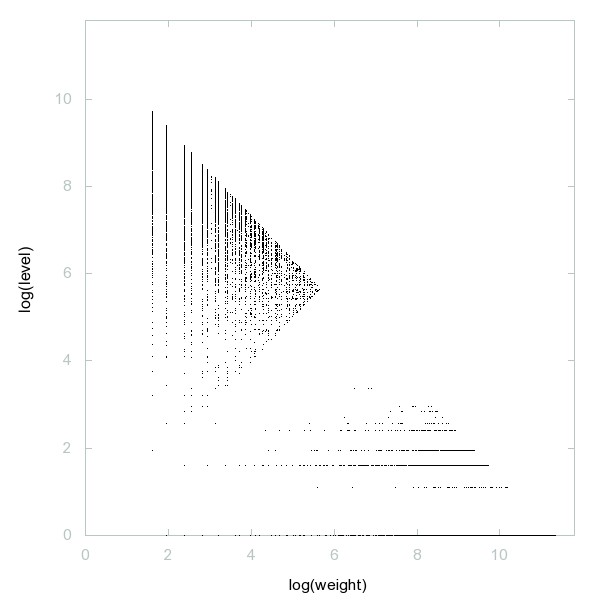
Decomposition of A033207

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes of form x^2+7*y^2.
A033207(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A033207 (9999 lines.)
Decomposition of A033207 - 9997 dots.

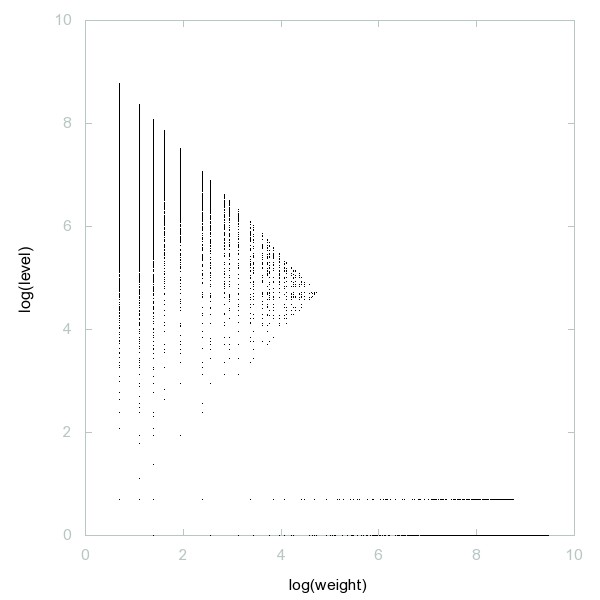
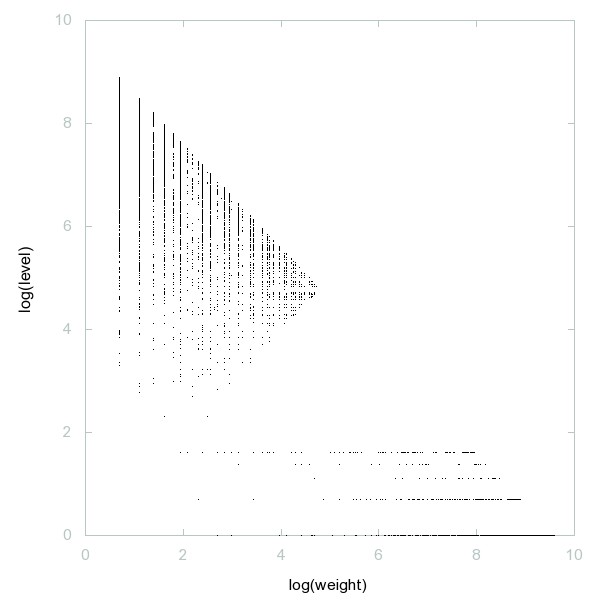
Decomposition of A033210

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes of the form x^2+13*y^2.
A033210(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A033210 (9999 lines.)
Decomposition of A033210 - 9996 dots.

Decomposition of A033556

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
a(n+1) = 2a(n) - {largest prime < a(n)}.
A033556(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A033556 (9999 lines.)
Decomposition of A033556 - 9999 dots.

Decomposition of A033948

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers that have a primitive root (the multiplicative group modulo n is cyclic).
A033948(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A033948 (9999 lines.)
Decomposition of A033948 - 9997 dots.

Decomposition of A033949

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Positive integers that do not have a primitive root.
A033949(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A033949 (9999 lines.)
Decomposition of A033949 - 9998 dots.

Decomposition of Refactorable numbers

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Refactorable numbers: number of divisors of n divides n. Also known as tau numbers.
A033950(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of Refactorable numbers (9999 lines.)
Decomposition of Refactorable numbers - 9995 dots.

Decomposition of A034017

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers that are primitively represented by x^2 + xy + y^2.
A034017(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A034017 (9999 lines.)
Decomposition of A034017 - 9995 dots.

Decomposition of A034020

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Not of the form x^2 + x*y + y^2.
A034020(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A034020 (9999 lines.)
Decomposition of A034020 - 9998 dots.

Decomposition of A034048

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers with multiplicative digital root value 0.
A034048(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A034048 (9999 lines.)
Decomposition of A034048 - 9997 dots.