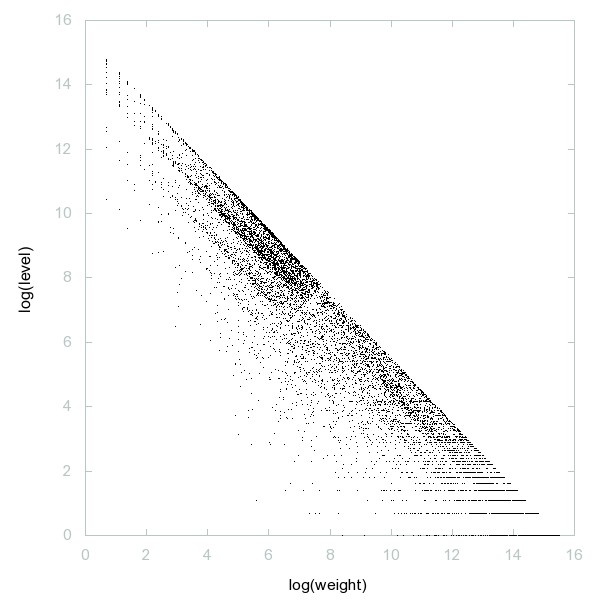
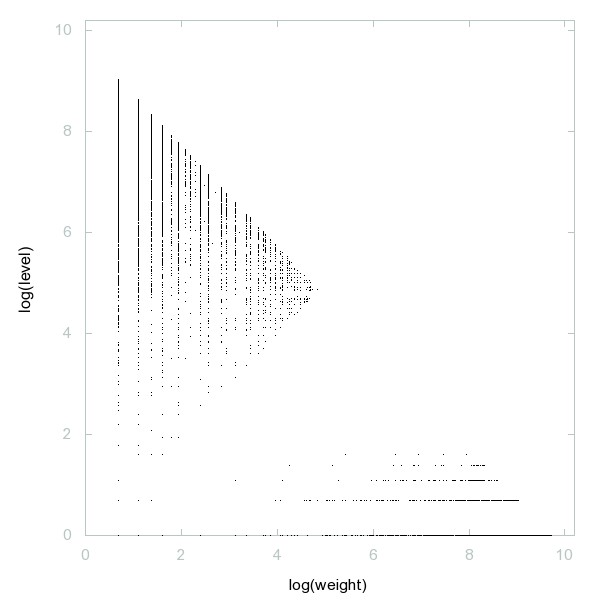
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of A260047

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Composites whose prime factorization in base 3 is an anagram of the number in base 3.
A260047(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A260047 (9999 lines.)
Decomposition of A260047 - 9994 dots.

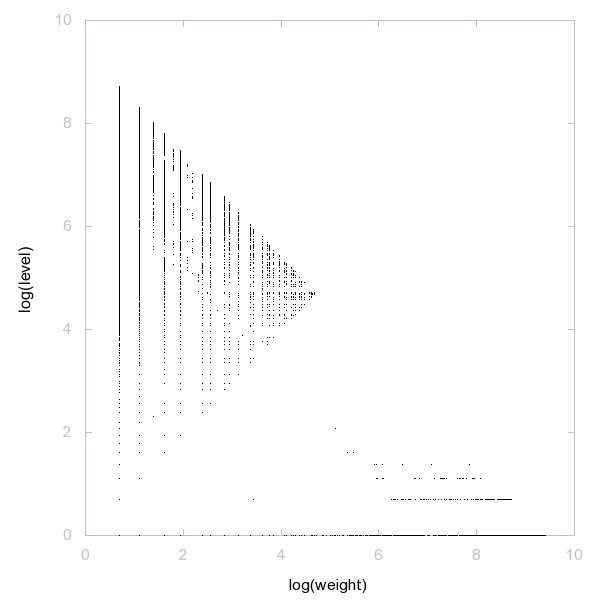
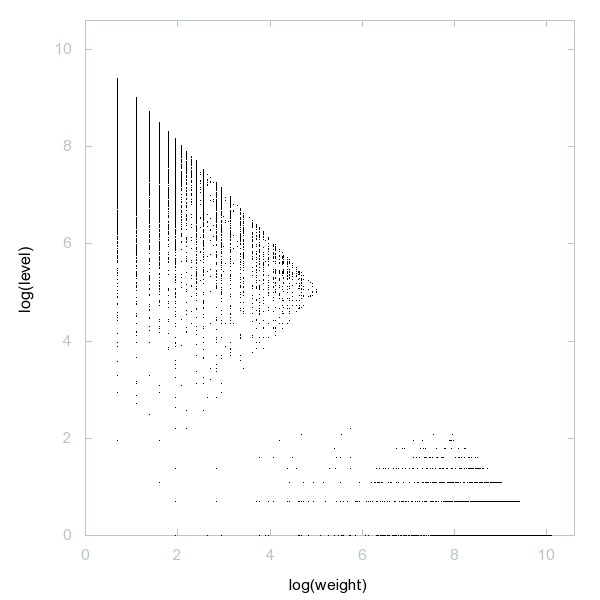
Decomposition of A260255

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers that can be written as the sum of two nonnegative palindromes in base 10.
A260255(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A260255 (9999 lines.)
Decomposition of A260255 - 9996 dots.

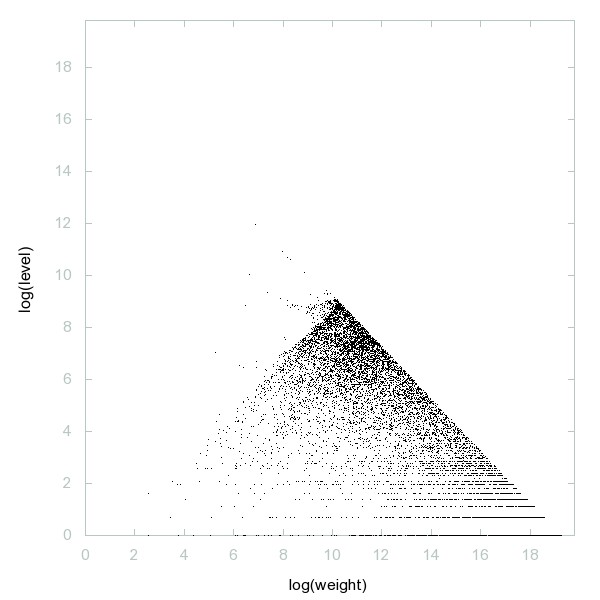
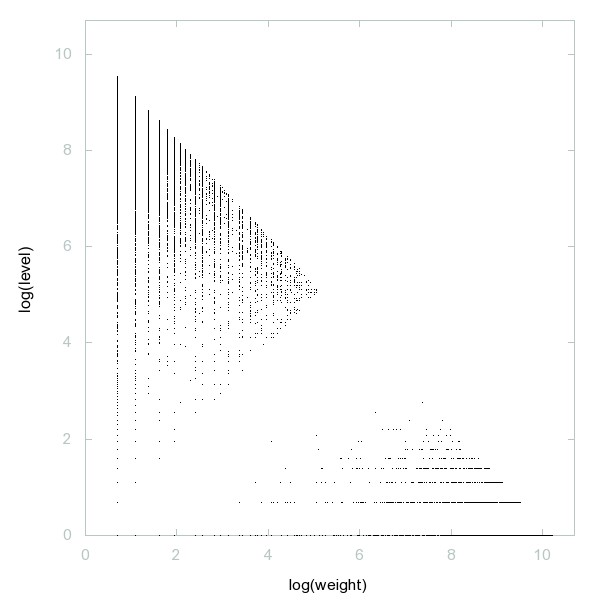
Decomposition of A260682

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Löschian numbers (A003136) of the form 6*k+1.
A260682(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A260682 (9999 lines.)
Decomposition of A260682 - 9997 dots.

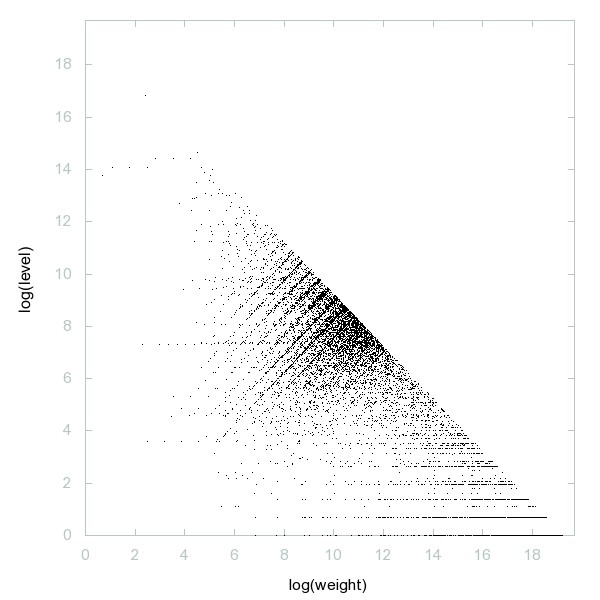
Decomposition of A262829

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
(3,2)-primes (defined in Comments).
A262829(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A262829 (9999 lines.)
Decomposition of A262829 - 9993 dots.

Decomposition of A267769

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers whose base 9 representation is a square when read in base 10.
A267769(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A267769 (9999 lines.)
Decomposition of A267769 - 9993 dots.

Decomposition of A267892

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers with 9 odd divisors.
A267892(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A267892 (9999 lines.)
Decomposition of A267892 - 9997 dots.

Decomposition of A270189

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n for which (prime(n+1)-prime(n)) is not a multiple of three.
A270189(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A270189 (9999 lines.)
Decomposition of A270189 - 9997 dots.

Decomposition of A270190

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n for which prime(n+1)-prime(n) is a multiple of three.
A270190(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A270190 (9999 lines.)
Decomposition of A270190 - 9999 dots.

Decomposition of A270297

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers which are representable as a sum of seven but no fewer consecutive nonnegative integers.
A270297(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A270297 (9999 lines.)
Decomposition of A270297 - 9996 dots.

Decomposition of A272159

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that abs(8n^2 - 488n + 7243) is prime.
A272159(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A272159 (9999 lines.)
Decomposition of A272159 - 9996 dots.