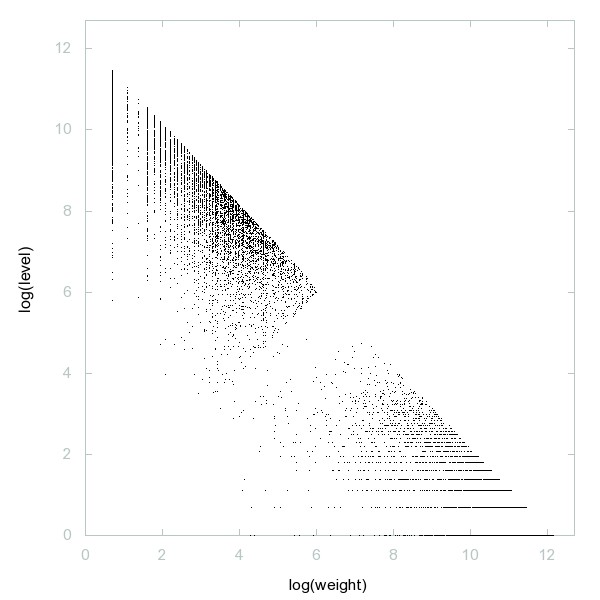
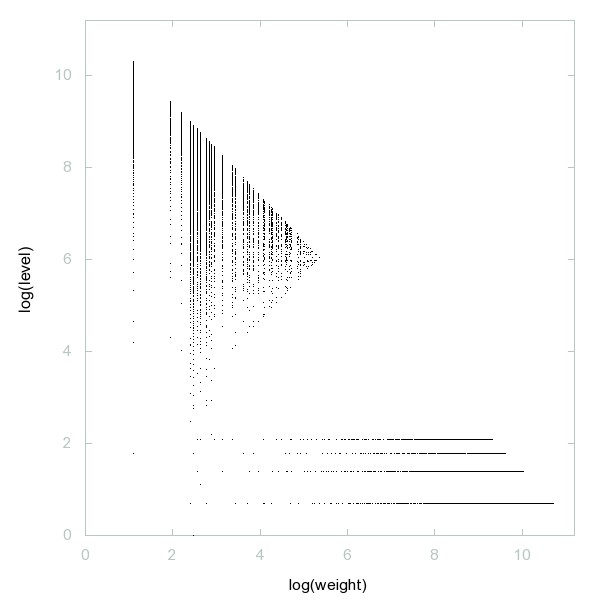
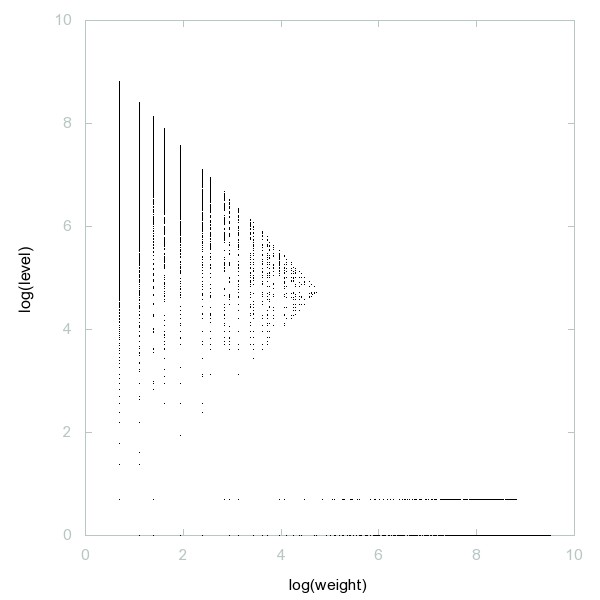
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of A274357

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that n and n+1 both have 8 divisors.
A274357(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A274357 (9999 lines.)
Decomposition of A274357 - 9999 dots.

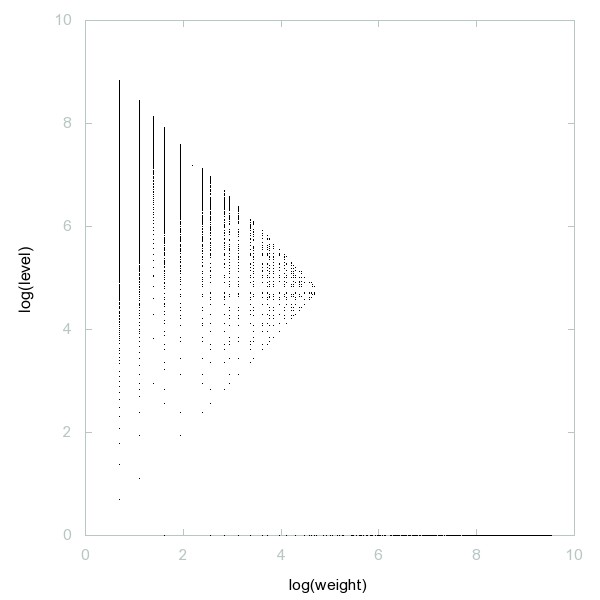
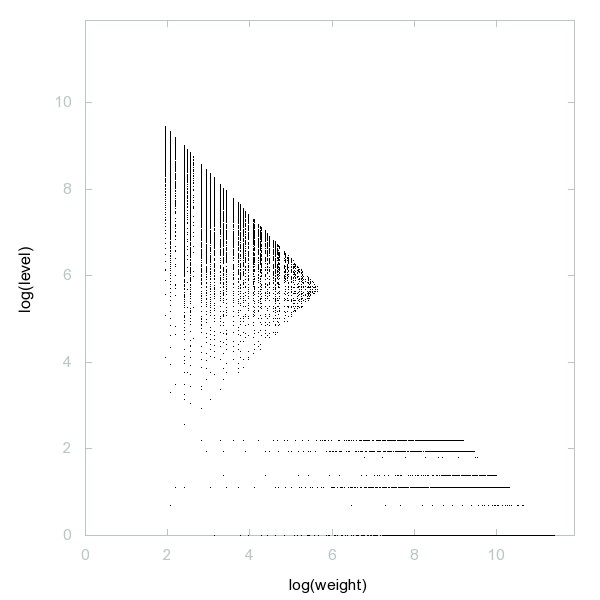
Decomposition of A276078

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n in whose prime factorization no exponent of any prime(k) exceeds k.
A276078(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A276078 (9999 lines.)
Decomposition of A276078 - 9996 dots.

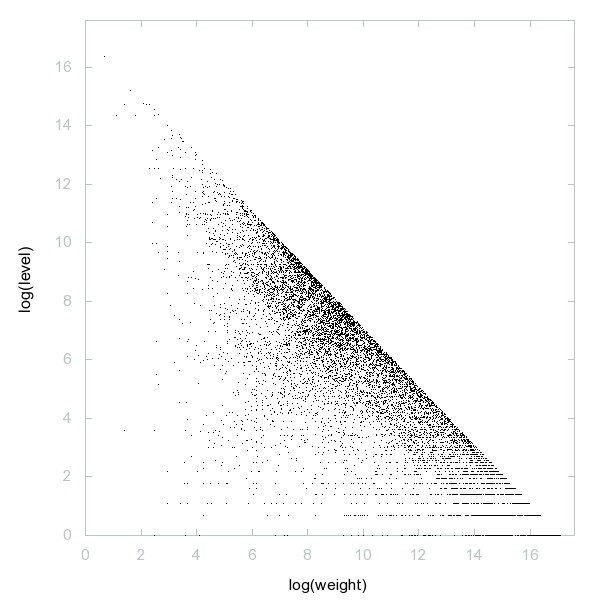
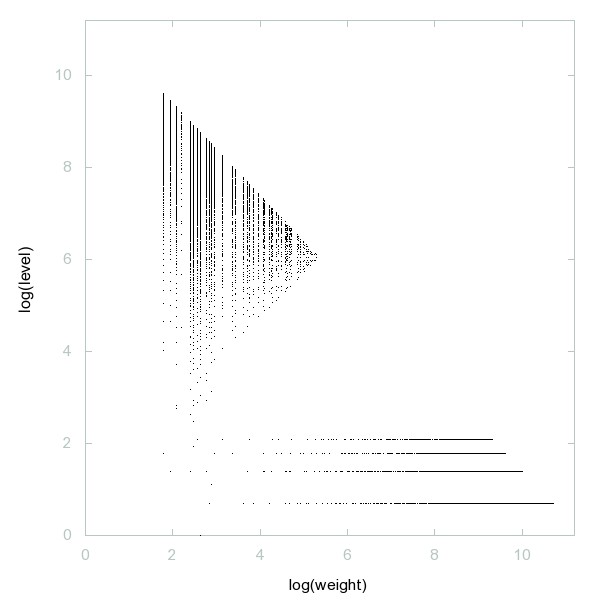
Decomposition of A276655

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that Sum_{p|n} 0.p is an integer where p ranges over the prime divisors of n.
A276655(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A276655 (9999 lines.)
Decomposition of A276655 - 9997 dots.

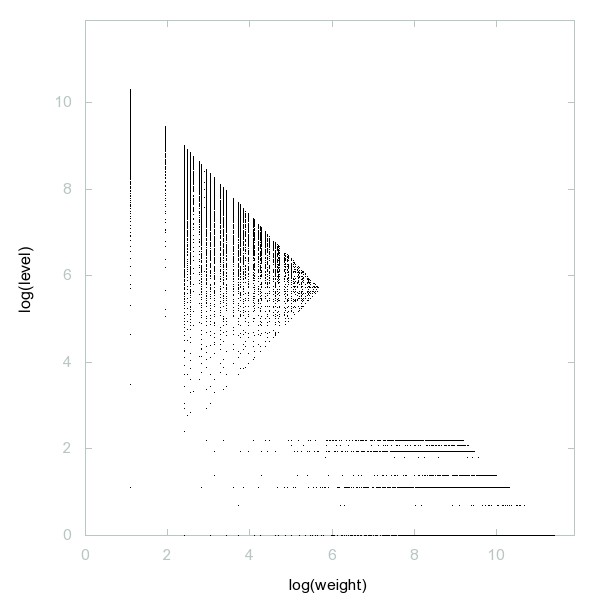
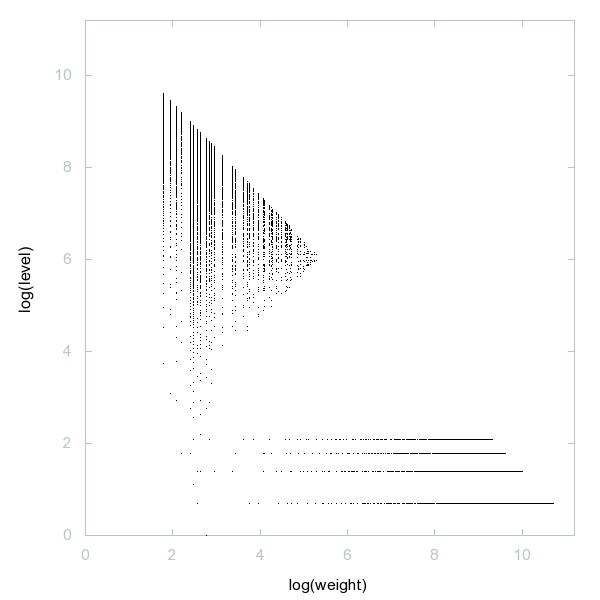
Decomposition of A277568

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that n/6^m == 2 mod 6, where 6^m is the greatest power of 6 that divides n.
A277568(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A277568 (9999 lines.)
Decomposition of A277568 - 9997 dots.

Decomposition of A277588

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers k such that k/10^m == 1 mod 10, where 10^m is the greatest power of 10 that divides n.
A277588(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A277588 (9999 lines.)
Decomposition of A277588 - 9997 dots.

Decomposition of A277589

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers k such that k/10^m == 2 mod 10, where 10^m is the greatest power of 10 that divides n.
A277589(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A277589 (9999 lines.)
Decomposition of A277589 - 9997 dots.

Decomposition of A277590

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers k such that k/10^m == 3 mod 10, where 10^m is the greatest power of 10 that divides n.
A277590(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A277590 (9999 lines.)
Decomposition of A277590 - 9997 dots.

Decomposition of A277591

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers k such that k/10^m == 4 mod 10, where 10^m is the greatest power of 10 that divides n.
A277591(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A277591 (9999 lines.)
Decomposition of A277591 - 9997 dots.

Decomposition of A277593

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers k such that k/10^m == 6 mod 10, where 10^m is the greatest power of 10 that divides n.
A277593(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A277593 (9999 lines.)
Decomposition of A277593 - 9997 dots.

Decomposition of A279607

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Beatty sequence for e/2; i.e., a(n) = floor(n*e/2).
A279607(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A279607 (9999 lines.)
Decomposition of A279607 - 9997 dots.