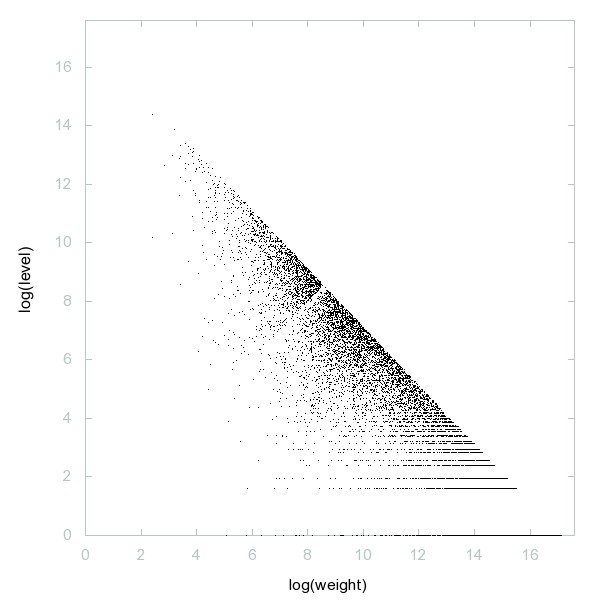
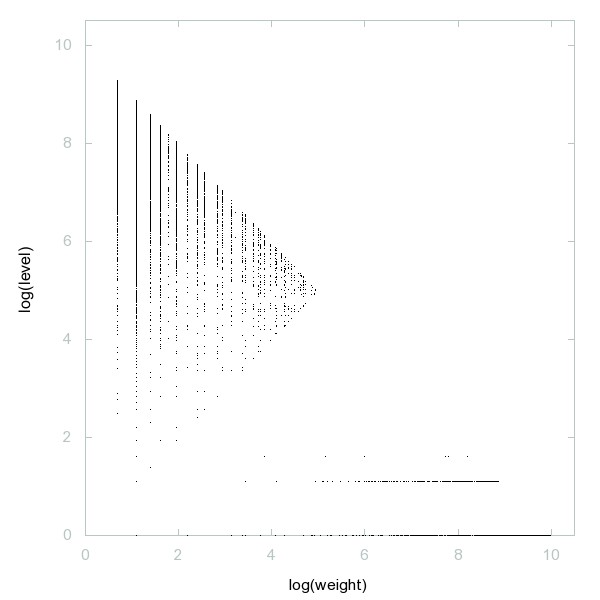
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of A235925

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes p with q = prime(p) - p + 1 and r = prime(q) - q + 1 both prime.
A235925(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A235925 (9999 lines.)
Decomposition of A235925 - 9993 dots.

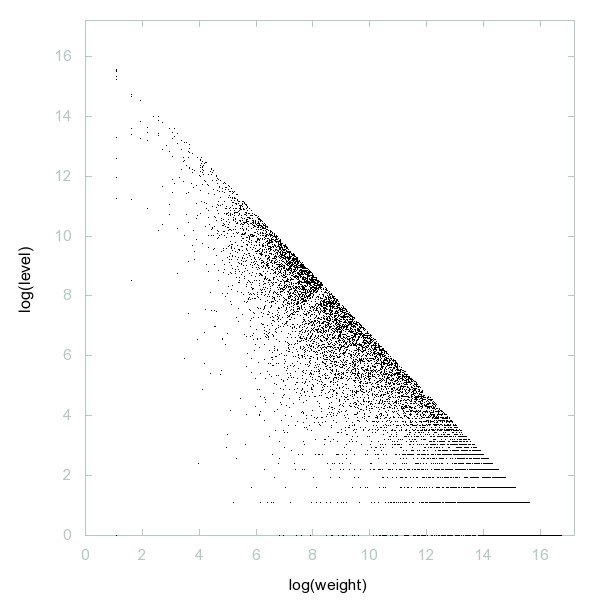
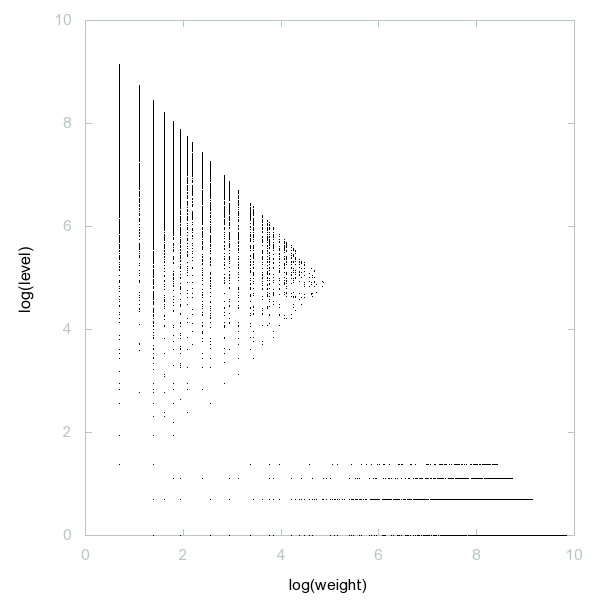
Decomposition of A236119

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes p with prime(p) - p - 1 and prime(p) - p + 1 both prime.
A236119(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A236119 (9999 lines.)
Decomposition of A236119 - 9993 dots.

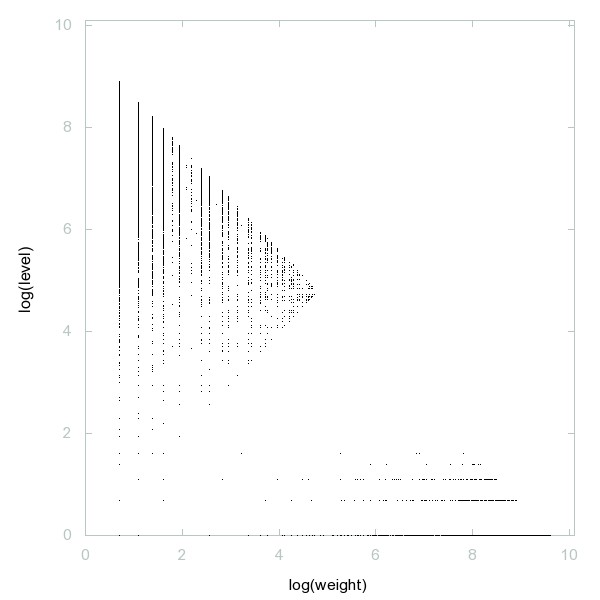
Decomposition of A236457

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes p with q = p + 2 and prime(q) + 2 both prime.
A236457(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A236457 (9999 lines.)
Decomposition of A236457 - 9993 dots.

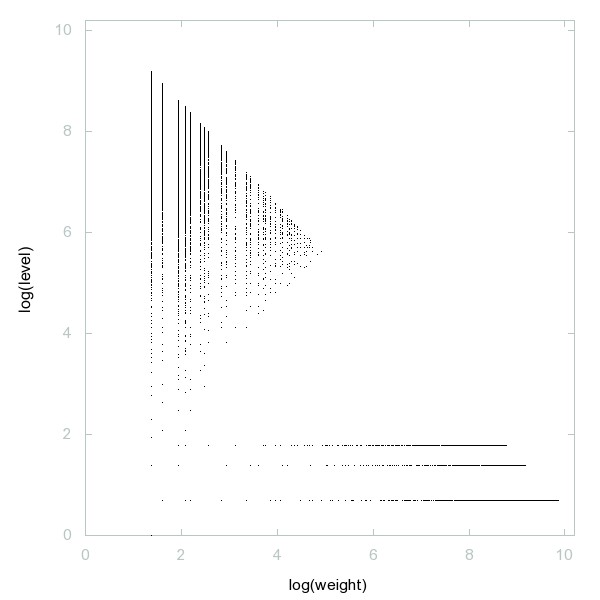
Decomposition of A236458

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes p with p + 2 and prime(p) + 2 both prime.
A236458(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A236458 (9999 lines.)
Decomposition of A236458 - 9995 dots.

Decomposition of A236464

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes p with prime(p) + 2 and prime(p) + 6 both prime.
A236464(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A236464 (9999 lines.)
Decomposition of A236464 - 9992 dots.

Decomposition of A236562

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that A049820(x) = n has a solution.
A236562(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A236562 (9999 lines.)
Decomposition of A236562 - 9995 dots.

Decomposition of A242414

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers whose prime factorization viewed as a tuple of nonzero powers is palindromic.
A242414(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A242414 (9999 lines.)
Decomposition of A242414 - 9997 dots.

Decomposition of A243937

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Even numbers n>=6 for which lpf(n-1) > lpf(n-3), where lpf = least prime factor.
A243937(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A243937 (9999 lines.)
Decomposition of A243937 - 9998 dots.

Decomposition of A246281

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that if n = product_{k >= 1} (p_k)^(c_k), then product_{k >= 1} (p_{k+1})^(c_k) < 2*n, where p_k indicates the k-th prime, A000040(k).
A246281(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A246281 (9999 lines.)
Decomposition of A246281 - 9995 dots.

Decomposition of A246282

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that if n = product_{k >= 1} (p_k)^(c_k), then product_{k >= 1} (p_{k+1})^(c_k) > 2*n, where p_k indicates the k-th prime, A000040(k).
A246282(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A246282 (9999 lines.)
Decomposition of A246282 - 9998 dots.