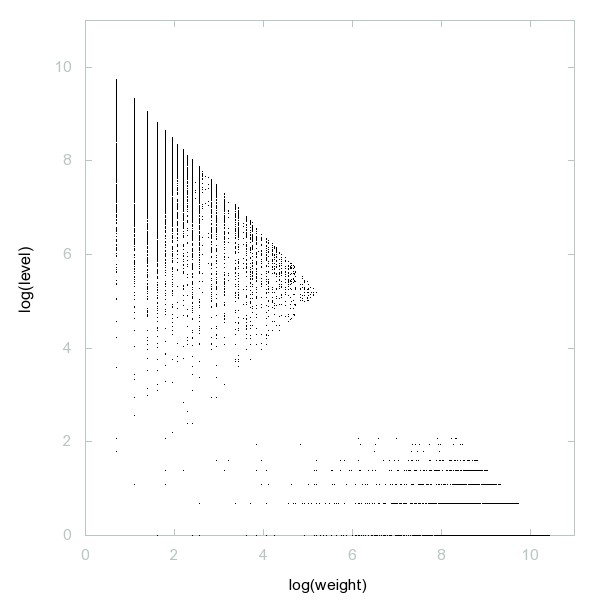
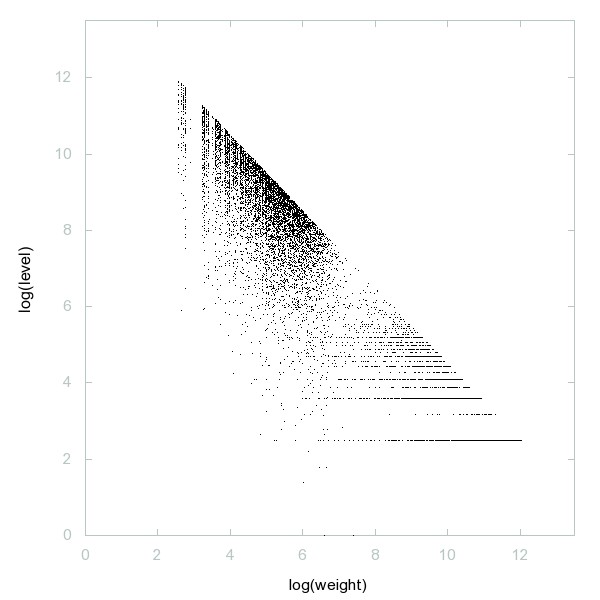
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of A246371

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that, if 2n-1 = Product_{k >= 1} (p_k)^(c_k) then n > Product_{k >= 1} (p_{k-1})^(c_k), where p_k indicates the k-th prime, A000040(k).
A246371(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A246371 (9999 lines.)
Decomposition of A246371 - 9998 dots.

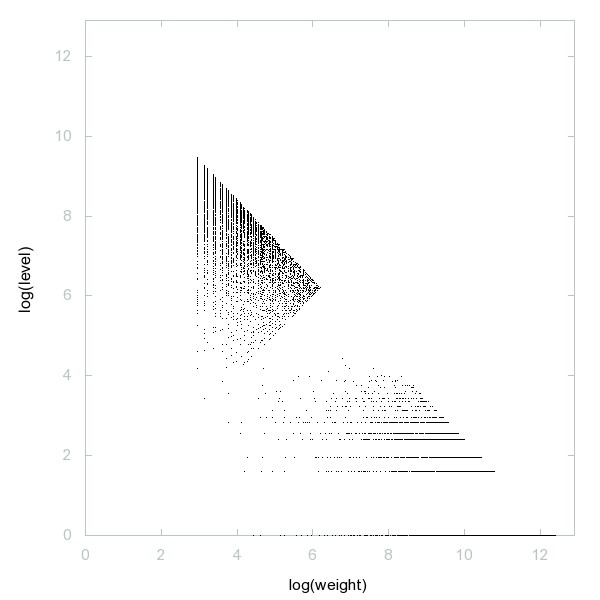
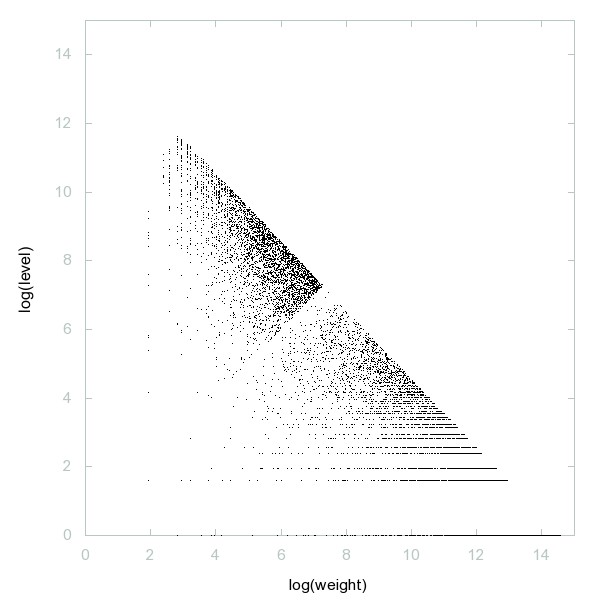
Decomposition of A247676

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Odd composite numbers congruent to 2 modulo 9.
A247676(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A247676 (9999 lines.)
Decomposition of A247676 - 9998 dots.

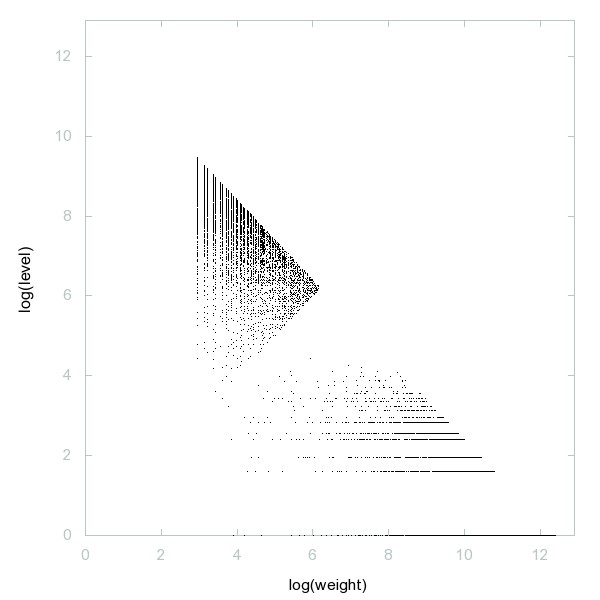
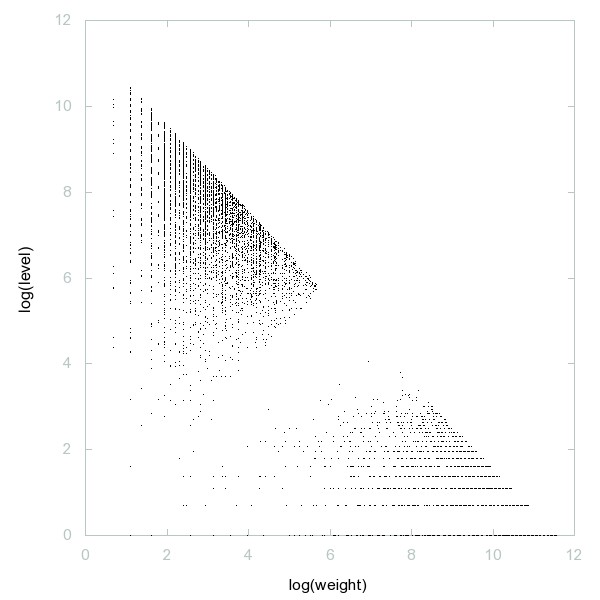
Decomposition of A247678

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Odd composite numbers congruent to 4 modulo 9.
A247678(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A247678 (9999 lines.)
Decomposition of A247678 - 9998 dots.

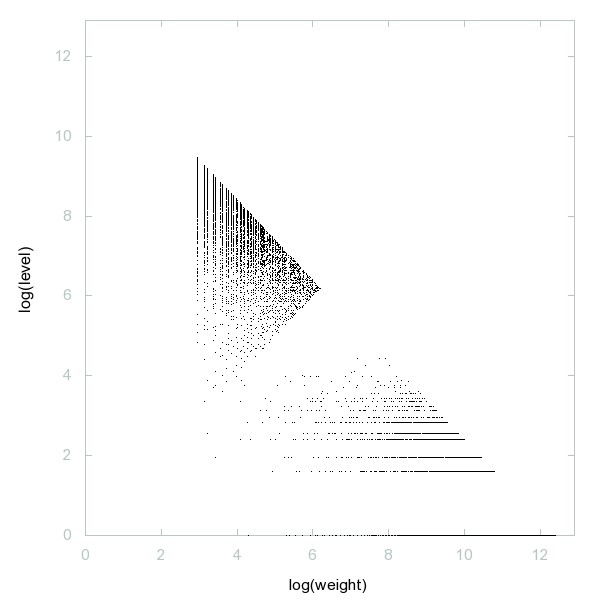
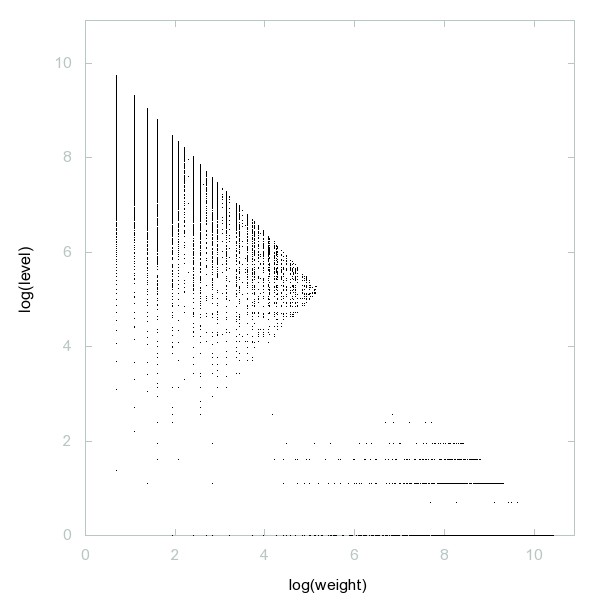
Decomposition of A247681

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Odd nonprimes congruent to 1 modulo 9.
A247681(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A247681 (9999 lines.)
Decomposition of A247681 - 9996 dots.

Decomposition of A248201

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that n-1, n and n+1 are all squarefree semiprimes.
A248201(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A248201 (9999 lines.)
Decomposition of A248201 - 9997 dots.

Decomposition of A248202

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Sphenic numbers (A007304) whose neighbors are sphenic.
A248202(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A248202 (9999 lines.)
Decomposition of A248202 - 9999 dots.

Decomposition of A249134

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that Bernoulli number B_n has denominator 2730.
A249134(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A249134 (9999 lines.)
Decomposition of A249134 - 9997 dots.

Decomposition of A249374

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Prime numbers Q such that the concatenation Q,1,Q is prime.
A249374(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A249374 (9999 lines.)
Decomposition of A249374 - 9996 dots.

Decomposition of A249669

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
a(n) = floor(prime(n)^(1+1/n)).
A249669(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A249669 (9999 lines.)
Decomposition of A249669 - 9997 dots.

Decomposition of A249723

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that there is a multiple of 9 on row n of Pascal's triangle with property that all multiples of 4 on the same row (if they exist) are larger than it.
A249723(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A249723 (9999 lines.)
Decomposition of A249723 - 9999 dots.