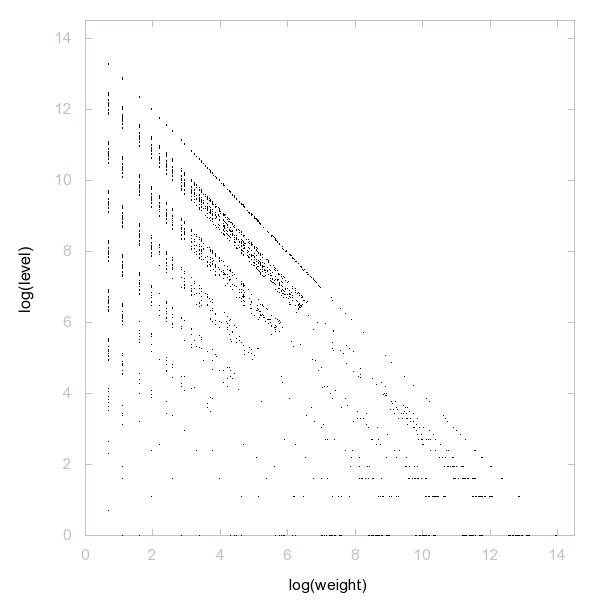
Decomposition of A250036
Numbers n such that m = floor(n/4) is coprime to n and, if nonzero, m is also a term of the sequence.
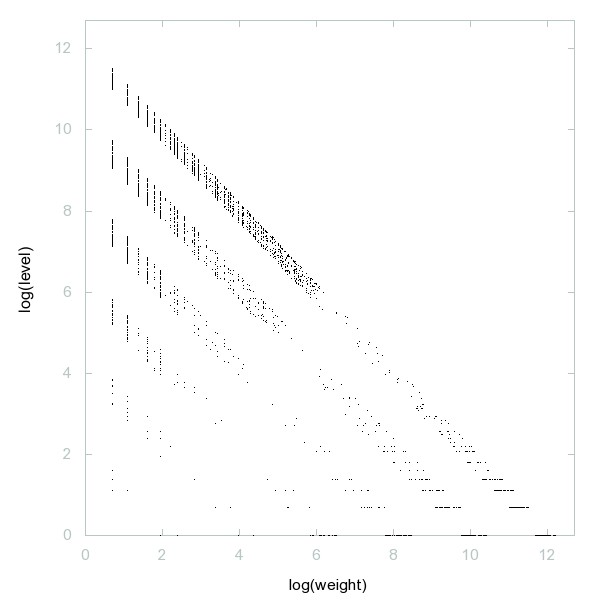
Decomposition of A250046
Numbers n such that m = floor(n/7) is coprime to n and, if nonzero, m is also a term of the sequence.
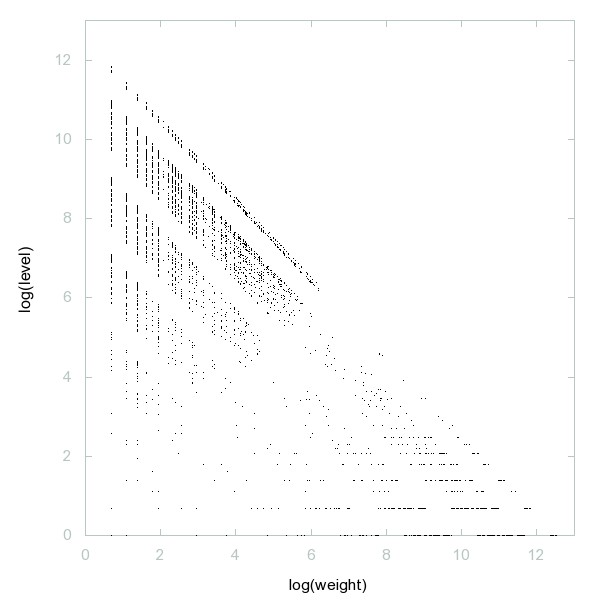
Decomposition of A250047
Numbers n such that m = floor(n/7) is not coprime to n and, if nonzero, m is also a term of the sequence.
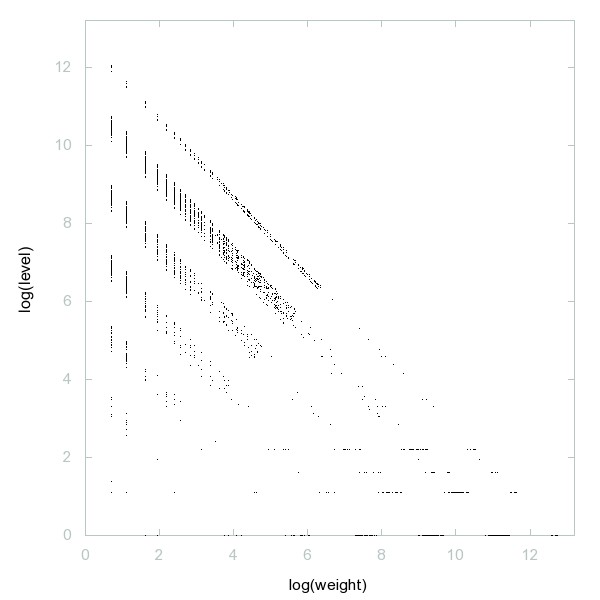
Decomposition of A250048
Numbers n such that m = floor(n/6) is coprime to n and, if nonzero, m is also a term of the sequence.
Decomposition of A250049
Numbers n such that m = floor(n/6) is not coprime to n and, if nonzero, m is also a term of the sequence.
Decomposition of A250444
Numbers n such that gcd(n!, Fibonacci(n)) is prime.
Decomposition of A251726
Numbers n > 1 for which gpf(n) < lpf(n)^2, where lpf and gpf (smallest and greatest prime factor of n) are given by A020639(n) and A006530(n).
Decomposition of A251728
Semiprimes p*q for which p <= q < p^2.
Decomposition of A256091
Numbers D such that D^2 = A^3 + B^4 + C^5 for some positive integers A, B, C.
Decomposition of Congrua
Congrua (possible solutions to the congruum problem): numbers n such that there are integers x, y and z with n = x^2-y^2 = z^2-x^2.