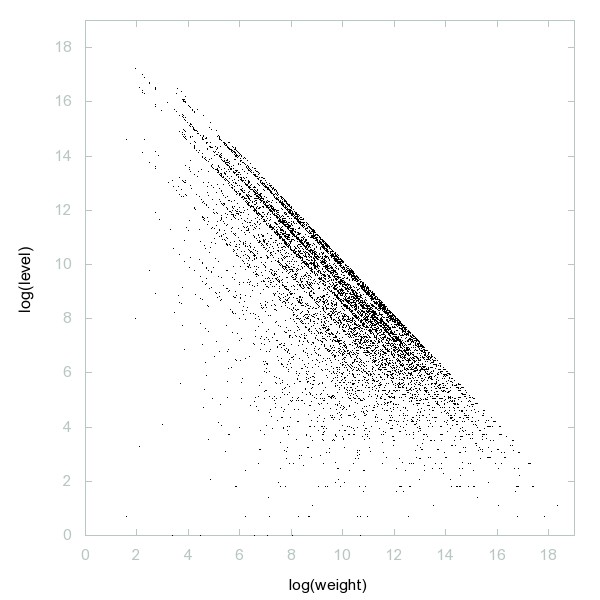
Decomposition of A256601
Numbers n such that the decimal expansions of both n and n^2 have 1 as smallest digit and 9 as largest digit.
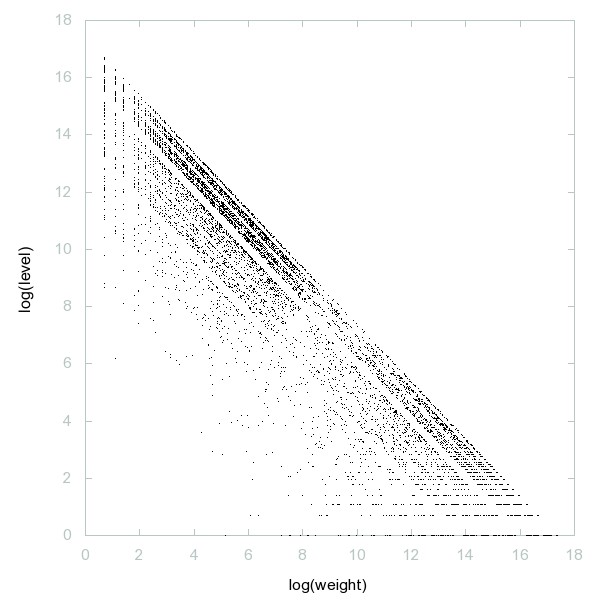
Decomposition of A256634
Numbers n such that the decimal expansions of both n and n^2 have 0 as smallest digit and 7 as largest digit.
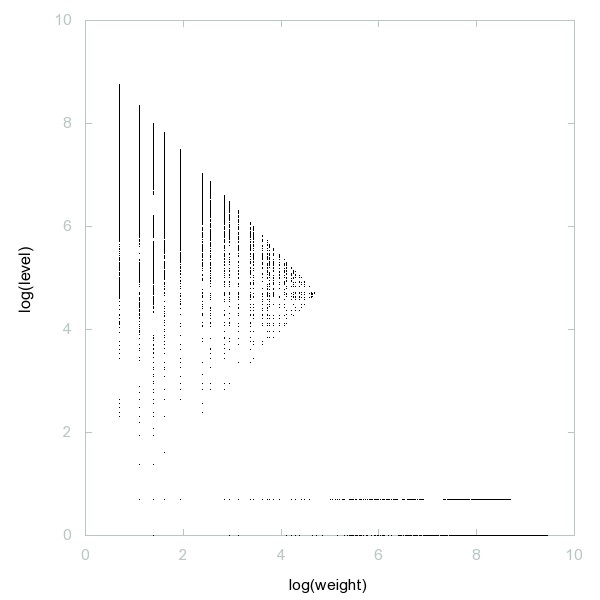
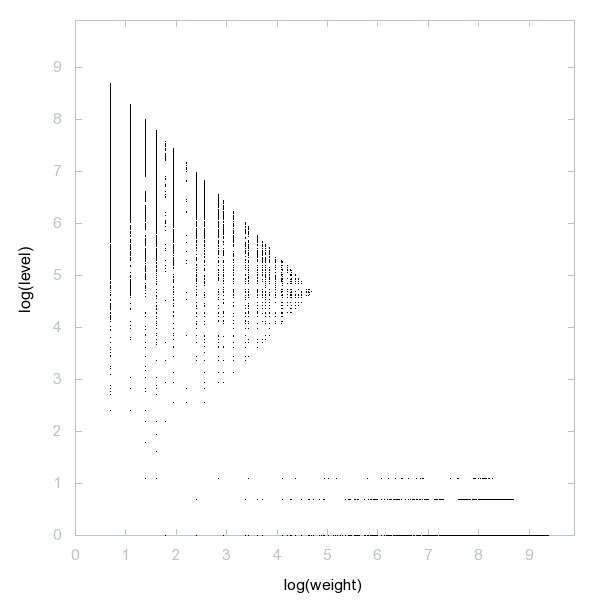
Decomposition of A256786
Numbers which are divisible by prime(d) for all digits d in their decimal representation.
Decomposition of A257210
Numbers n such that the decimal expansions of both n and n^2 have 1 as smallest digit and 7 as largest digit.
Decomposition of A257211
Numbers n such that the decimal expansions of both n and n^2 have 1 as smallest digit and 8 as largest digit.
Decomposition of A257219
Numbers n that have at least one divisor containing the digit 2 in base 10.
Decomposition of A257220
Numbers n that have at least one divisor containing the digit 3 in base 10.
Decomposition of A257368
Numbers n such that the decimal expansions of both n and n^2 have 2 as smallest digit and 8 as largest digit.
Decomposition of A258024
Natural numbers n such that the iteration of the function floor(tan(k)) applied to n eventually reaches [the fixed point] 1 (or any larger integer if such fixed points exist), where k is interpreted as k radians.
Decomposition of A260046
Composites whose prime factorization in base 2 is an anagram of the number in base 2.