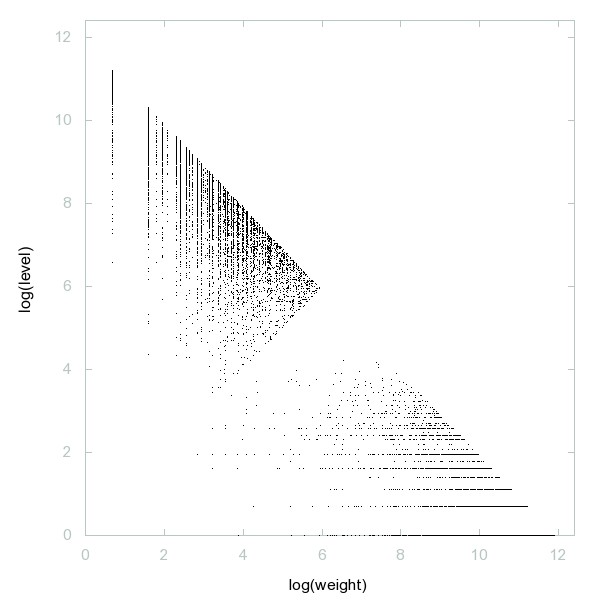
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of A195943

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Zeroless prime powers: Intersection of A000961 and A052382.
A195943(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A195943 (9999 lines.)
Decomposition of A195943 - 9997 dots.

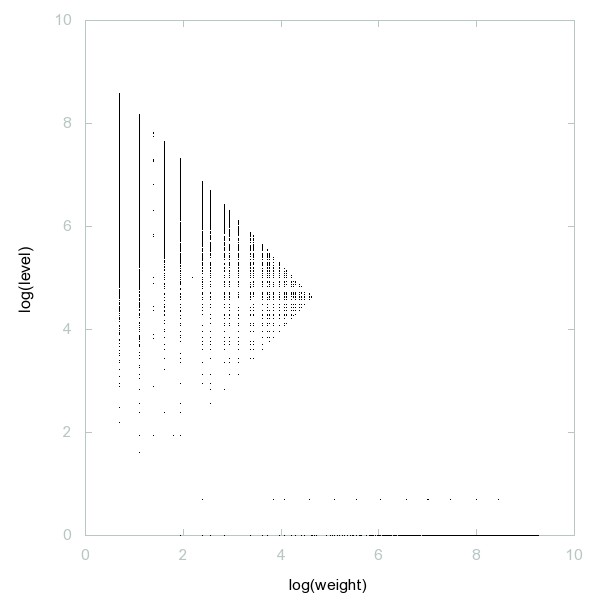
Decomposition of A196667

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
The Chebyshev primes of index 1.
A196667(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A196667 (9999 lines.)
Decomposition of A196667 - 9999 dots.

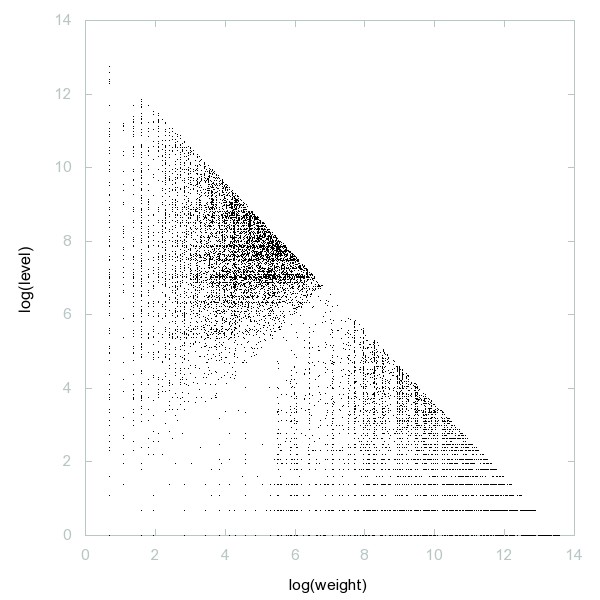
Decomposition of A198273

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes not of the form p*q + p + q for any primes p and q.
A198273(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A198273 (9999 lines.)
Decomposition of A198273 - 9995 dots.

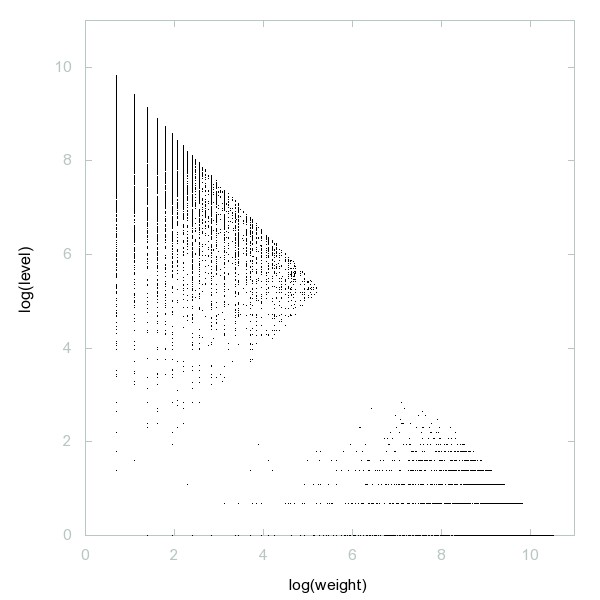
Decomposition of A198772

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers having exactly one representation by the quadratic form x^2+xy+y^2 with 0<=x<=y.
A198772(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A198772 (9999 lines.)
Decomposition of A198772 - 9996 dots.

Decomposition of A198773

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers having exactly two representations by the quadratic form x^2+xy+y^2 with 0<=x<=y.
A198773(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A198773 (9999 lines.)
Decomposition of A198773 - 9998 dots.

Decomposition of A200995

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers not expressible as a product of Lucas numbers.
A200995(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A200995 (9999 lines.)
Decomposition of A200995 - 9998 dots.

Decomposition of A201010

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Integers that can be written as the product and/or quotient of Lucas numbers.
A201010(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A201010 (9999 lines.)
Decomposition of A201010 - 9996 dots.

Decomposition of A201012

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Integers that cannot be written as the product and/or quotient of Lucas numbers.
A201012(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A201012 (9999 lines.)
Decomposition of A201012 - 9998 dots.

Decomposition of A201817

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that 90*n + 67 is prime.
A201817(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A201817 (9999 lines.)
Decomposition of A201817 - 9996 dots.

Decomposition of A202267

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers in which all digits are noncomposites (1, 2, 3, 5, 7) or 0.
A202267(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A202267 (9999 lines.)
Decomposition of A202267 - 9995 dots.