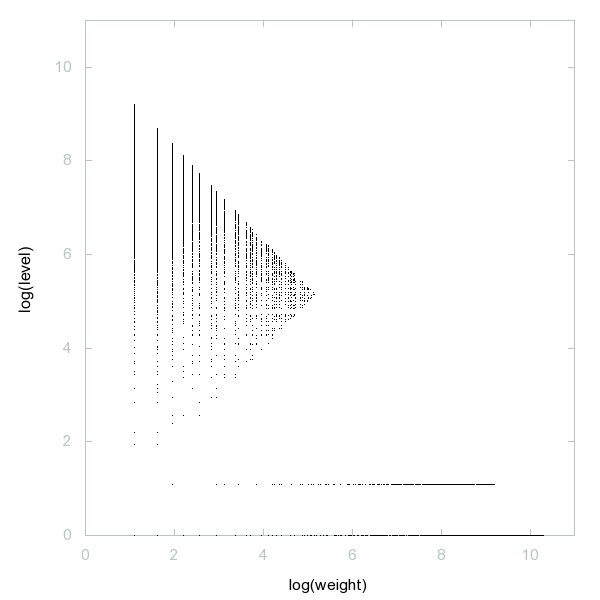
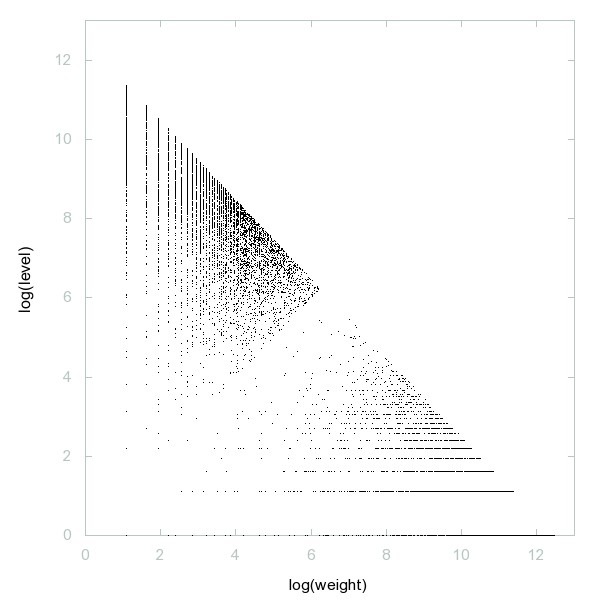
Decomposition of A079000
a(n) is taken to be the smallest positive integer greater than a(n-1) which is consistent with the condition "n is a member of the sequence if and only if a(n) is odd".
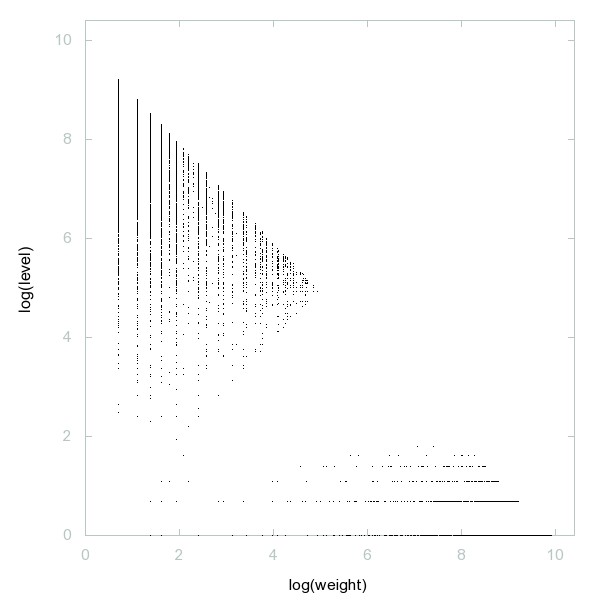
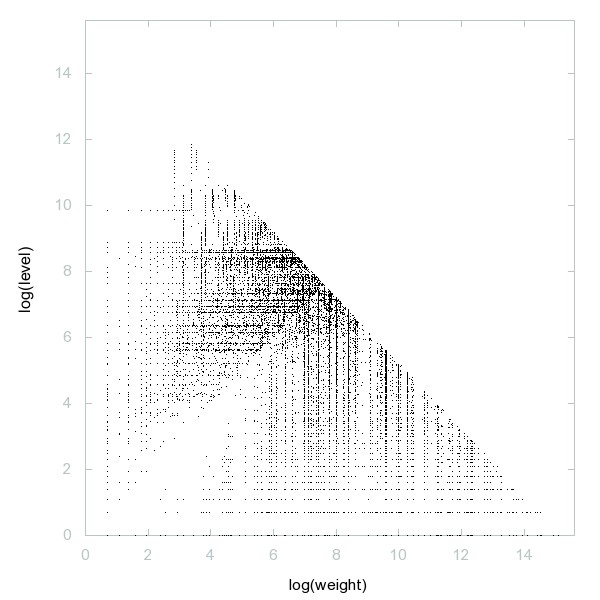
Decomposition of A079523
Numbers n such that binary representation ends in an odd number of ones.
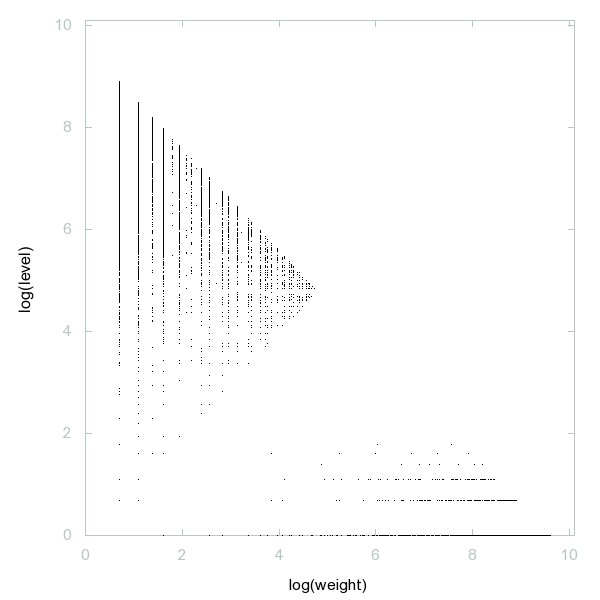
Decomposition of A079545
Primes of the form x^2 + y^2 + 1 with x,y >= 0.
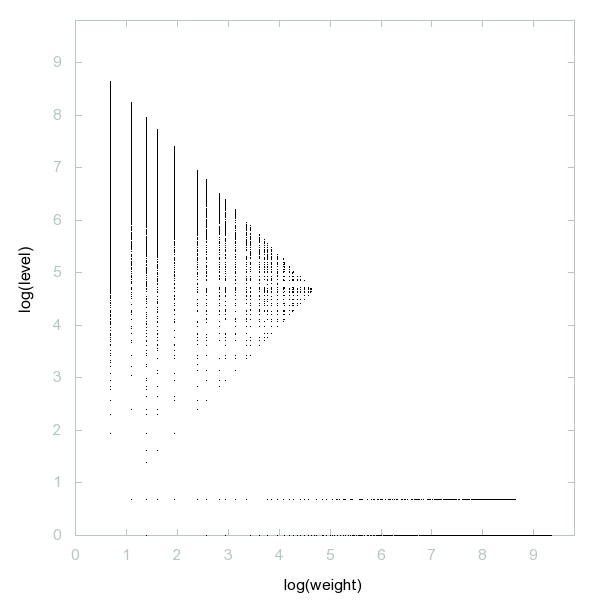
Decomposition of Proth numbers
Proth numbers: of the form k*2^m + 1 for k odd, m >= 1 and 2^m > k.
Decomposition of A080147
Positions of 4k+1 primes A002144 among all primes A000040.
Decomposition of A080218
Monotonically increasing sequence such that every positive integer n appears if and only if d(n) doesn't (d(n)=number of divisors of n, A000005).
Decomposition of A080257
Numbers having at least two distinct or a total of at least three prime factors.
Decomposition of Deletable primes
Deletable primes: primes such that removing some digit leaves either the empty string or another deletable prime.
Decomposition of A080663
Numbers of the form 3*n^2 - 1.
Decomposition of A080681
17-smooth numbers: i.e. numbers whose prime divisors are all <= 17.