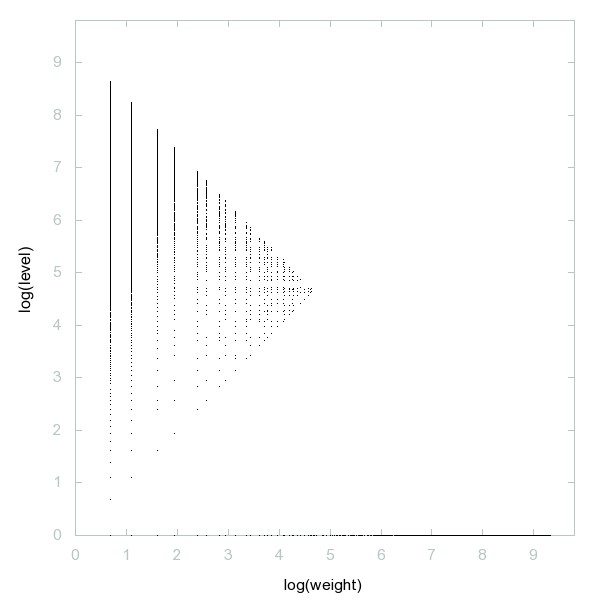
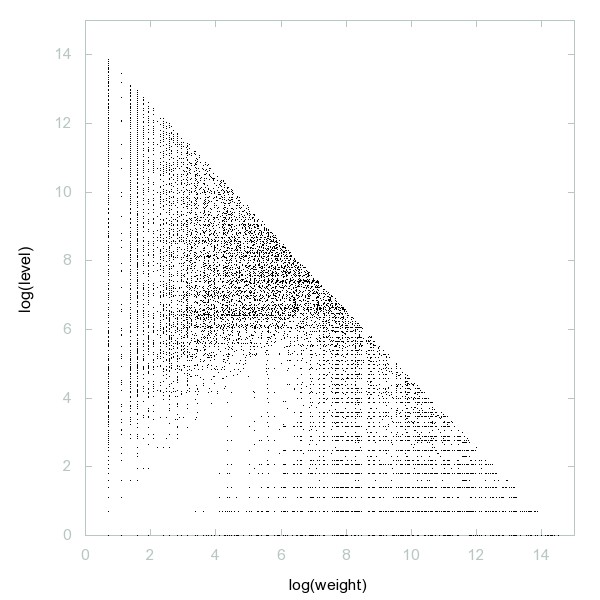
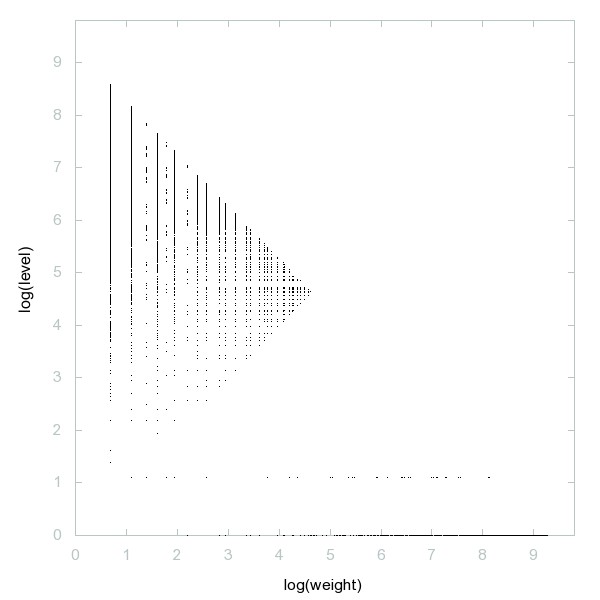
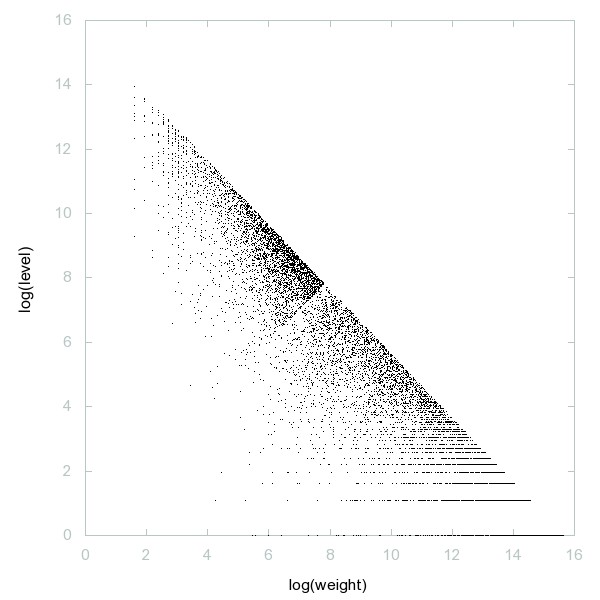
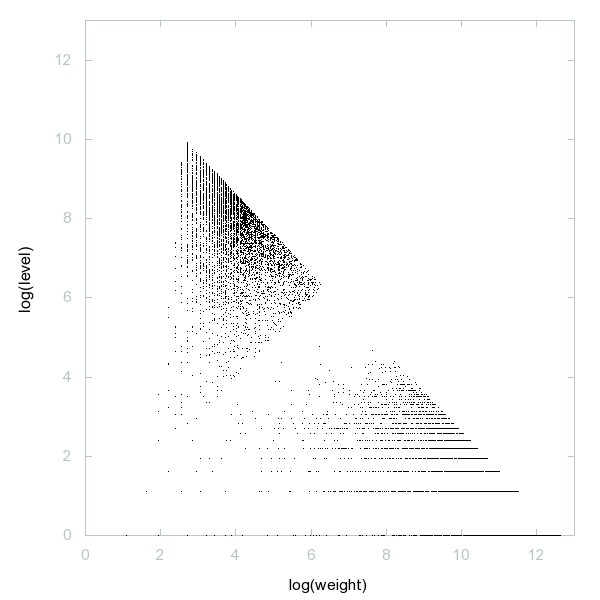
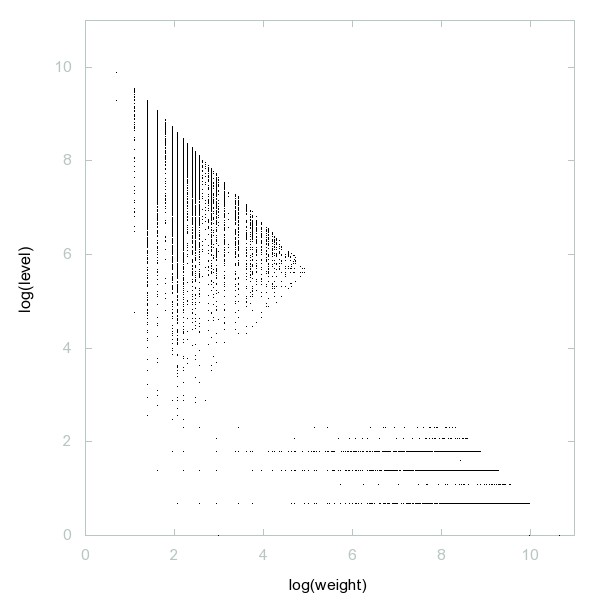
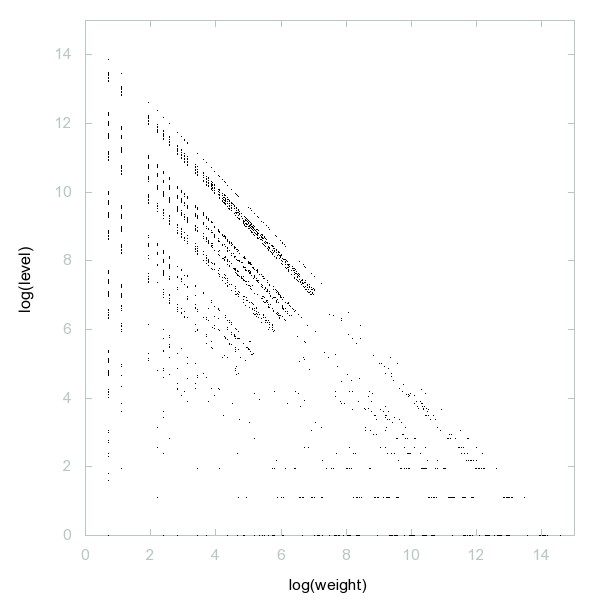
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of 23-smooth numbers

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
23-smooth numbers: i.e. numbers whose prime divisors are all <= 23.
A080683(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of 23-smooth numbers (9999 lines.)
Decomposition of 23-smooth numbers - 9997 dots.

Decomposition of A081092

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes having in binary representation a prime number of 1's.
A081092(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A081092 (9999 lines.)
Decomposition of A081092 - 9996 dots.

Decomposition of A081311

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers that can be written as sum of a prime and an 3-smooth number.
A081311(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A081311 (9999 lines.)
Decomposition of A081311 - 9999 dots.

Decomposition of A081330

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers that can be written as sum of two 3-smooth numbers.
A081330(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A081330 (9999 lines.)
Decomposition of A081330 - 9998 dots.

Decomposition of A081605

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers having at least one 0 in their ternary representation.
A081605(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A081605 (9999 lines.)
Decomposition of A081605 - 9996 dots.

Decomposition of A082077

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Balanced primes of order two.
A082077(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A082077 (9999 lines.)
Decomposition of A082077 - 9998 dots.

Decomposition of A082246

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes that are the sum of 7 consecutive primes.
A082246(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A082246 (9999 lines.)
Decomposition of A082246 - 9999 dots.

Decomposition of A082885

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes followed by a larger-than-average prime gap.
A082885(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A082885 (9999 lines.)
Decomposition of A082885 - 9996 dots.

Decomposition of Zumkeller numbers

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Zumkeller numbers: numbers n whose divisors can be partitioned into two disjoint sets whose sums are both sigma(n)/2.
A083207(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of Zumkeller numbers (9999 lines.)
Decomposition of Zumkeller numbers - 9997 dots.

Decomposition of A084544

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Alternate number system in base 4.
A084544(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A084544 (9999 lines.)
Decomposition of A084544 - 9990 dots.