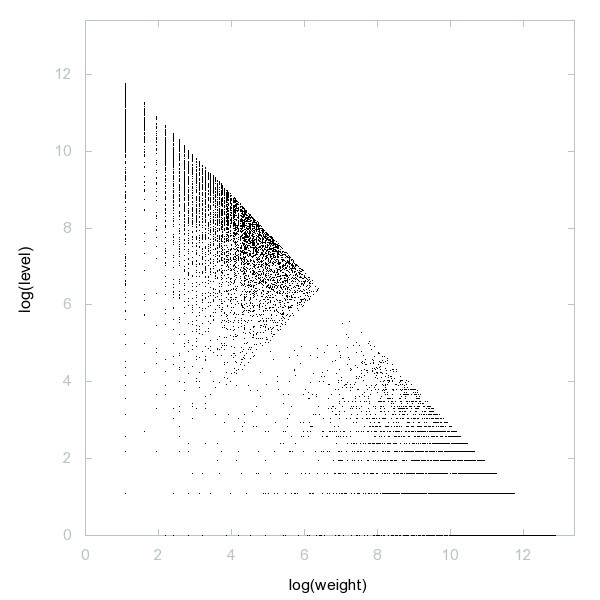
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of A049282

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes p such that both p-2 and p+2 are squarefree.
A049282(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A049282 (9999 lines.)
Decomposition of A049282 - 9996 dots.

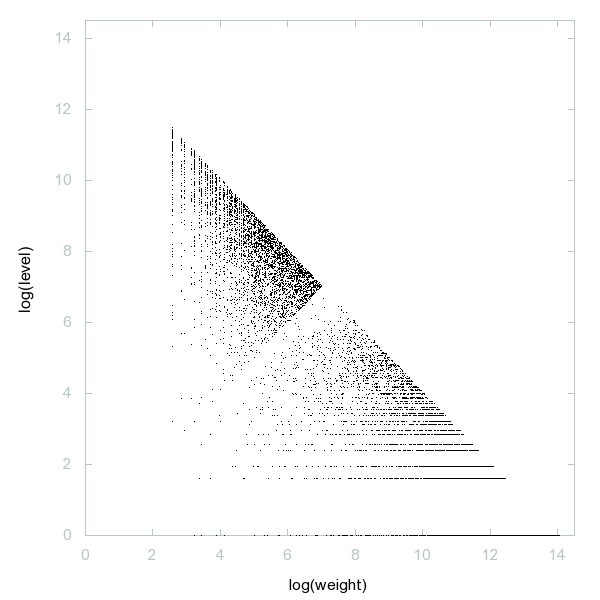
Decomposition of A049329

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that n is a substring of n^n.
A049329(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A049329 (9999 lines.)
Decomposition of A049329 - 9997 dots.

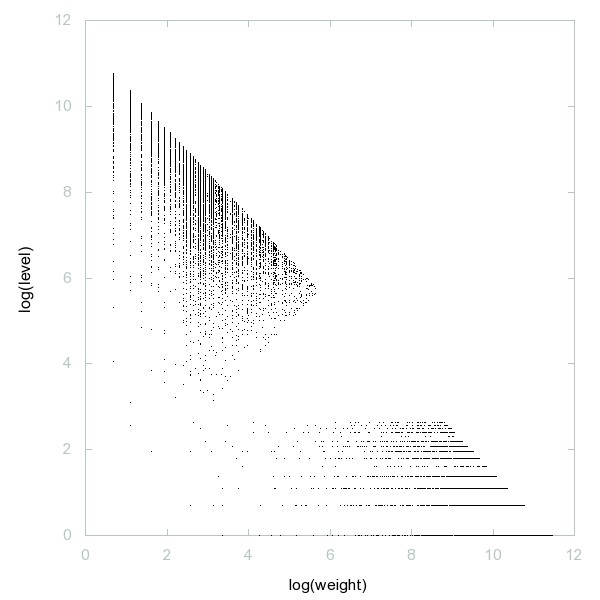
Decomposition of A049481

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Both p and p+30 are primes.
A049481(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A049481 (9999 lines.)
Decomposition of A049481 - 9998 dots.

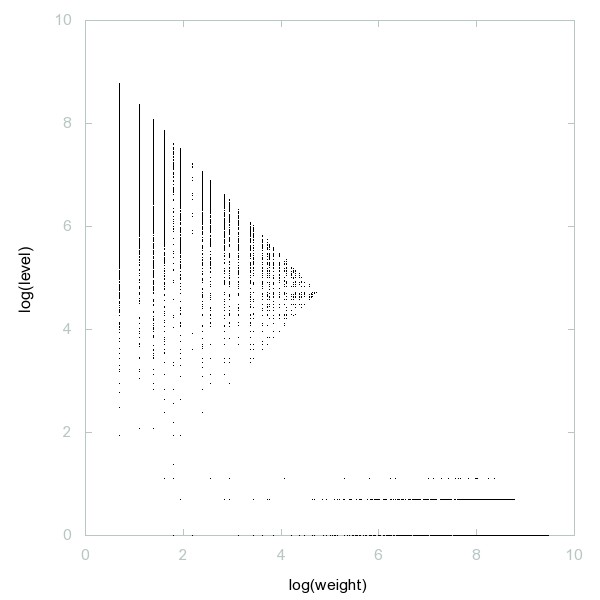
Decomposition of A049488

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes p such that p+16 is prime.
A049488(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A049488 (9999 lines.)
Decomposition of A049488 - 9994 dots.

Decomposition of A049532

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that n^2+1 is not squarefree.
A049532(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A049532 (10000 lines.)
Decomposition of A049532 - 9998 dots.

Decomposition of A050376

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers of the form p^(2^k) where p is prime and k >= 0.
A050376(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A050376 (9999 lines.)
Decomposition of A050376 - 9998 dots.

Decomposition of A050384

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Nonprimes such that n and phi(n) are relatively prime.
A050384(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A050384 (9999 lines.)
Decomposition of A050384 - 9997 dots.

Decomposition of A050435

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
a(n) = composite(composite(n)), where composite = A002808, composite numbers.
A050435(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A050435 (9999 lines.)
Decomposition of A050435 - 9999 dots.

Decomposition of A050695

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Composite numbers n such that none of the prime factors of n is a substring of n.
A050695(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A050695 (9999 lines.)
Decomposition of A050695 - 9998 dots.

Decomposition of A050795

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that n^2 - 1 is expressible as the sum of two nonzero squares in at least one way.
A050795(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A050795 (9999 lines.)
Decomposition of A050795 - 9996 dots.