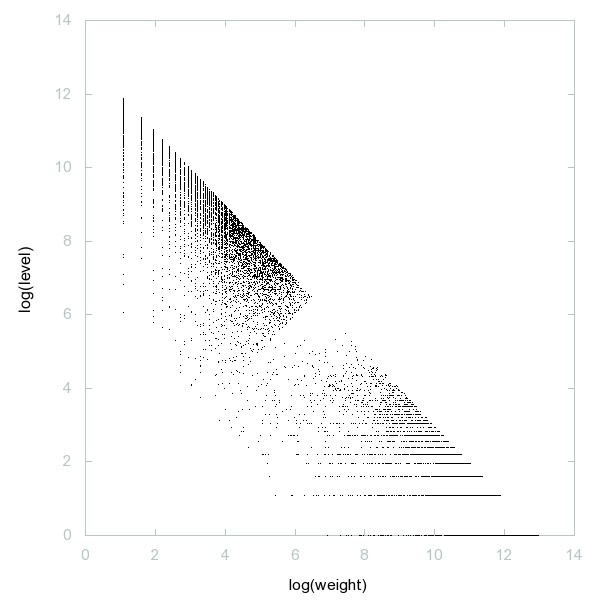
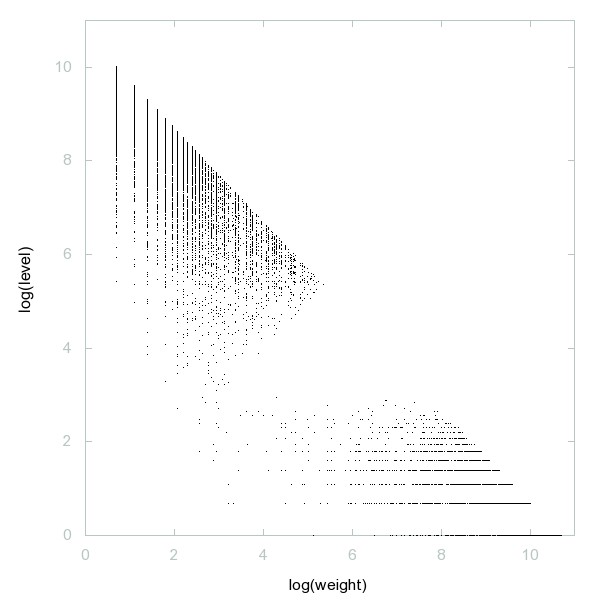
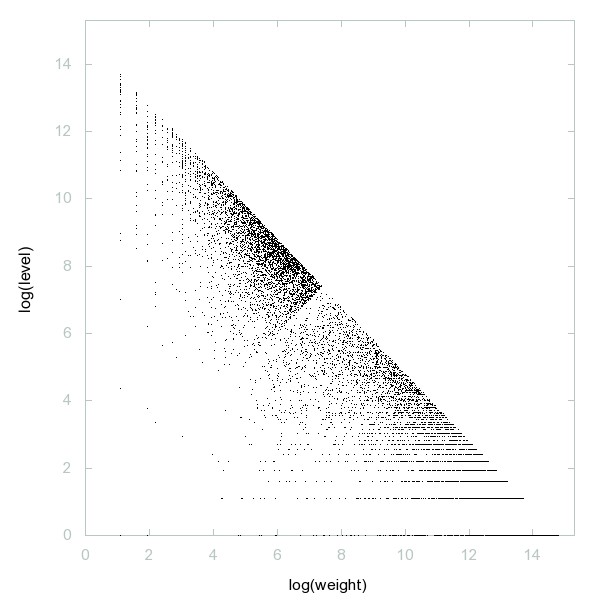
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of A050805

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Inserting any digit between adjacent digits of prime p never yields another prime.
A050805(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A050805 (9999 lines.)
Decomposition of A050805 - 9998 dots.

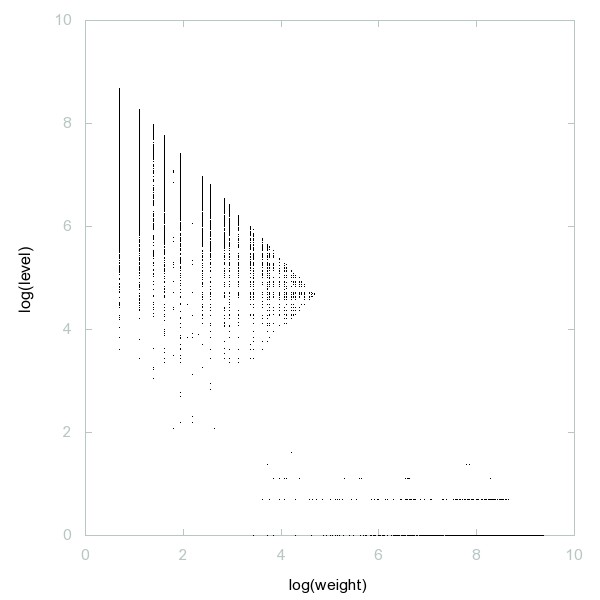
Decomposition of A050813

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n not palindromic in any base b, 2 <= b <= 10.
A050813(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A050813 (9999 lines.)
Decomposition of A050813 - 9998 dots.

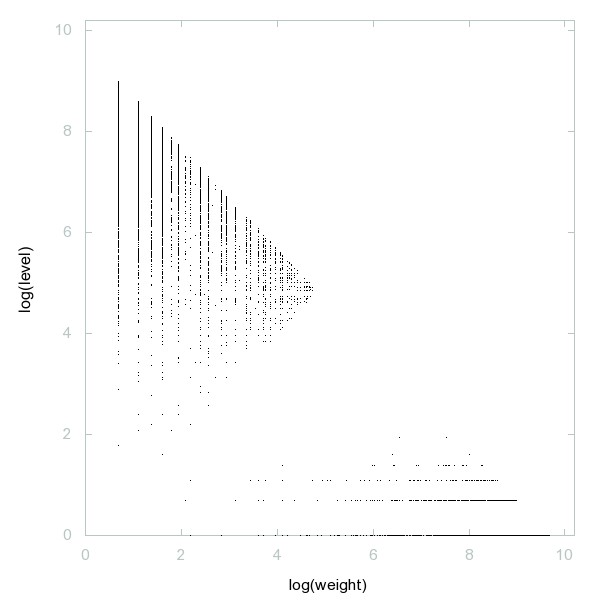
Decomposition of A050931

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Solutions c of cot(2*Pi/3)*(-(a+b+c)*(-a+b+c)*(-a+b-c)*(a+b-c))^(1/2)=a^2+b^2-c^2, c>a,b integers.
A050931(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A050931 (9999 lines.)
Decomposition of A050931 - 9998 dots.

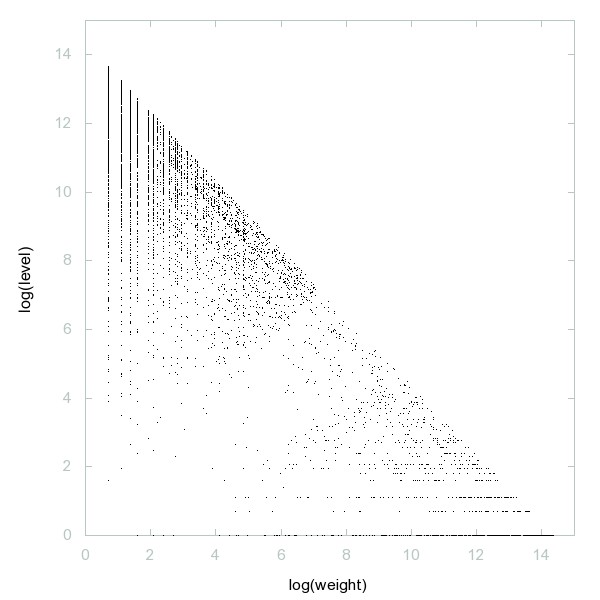
Decomposition of A050936

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Sum of two or more consecutive prime numbers.
A050936(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A050936 (9999 lines.)
Decomposition of A050936 - 9998 dots.

Decomposition of A051004

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers divisible both by their individual digits and by the sum of their digits.
A051004(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A051004 (9999 lines.)
Decomposition of A051004 - 9994 dots.

Decomposition of A051146

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Sequence b(n) mentioned in A051145.
A051146(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A051146 (9999 lines.)
Decomposition of A051146 - 9994 dots.

Decomposition of A051283

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that if write n = Product p_i^e_i (p_i primes) and P = max p_i^e_i, then n/P > P.
A051283(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A051283 (9999 lines.)
Decomposition of A051283 - 9998 dots.

Decomposition of A051507

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes p such that p*q+2 is prime, where q is next prime after p.
A051507(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A051507 (9999 lines.)
Decomposition of A051507 - 9995 dots.

Decomposition of Strong primes

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Strong primes: prime(n) > (prime(n-1) + prime(n+1))/2.
A051634(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of Strong primes (10000 lines.)
Decomposition of Strong primes - 9998 dots.

Decomposition of Weak primes

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Weak primes: prime(n) < (prime(n-1) + prime(n+1))/2.
A051635(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of Weak primes (10000 lines.)
Decomposition of Weak primes - 9998 dots.