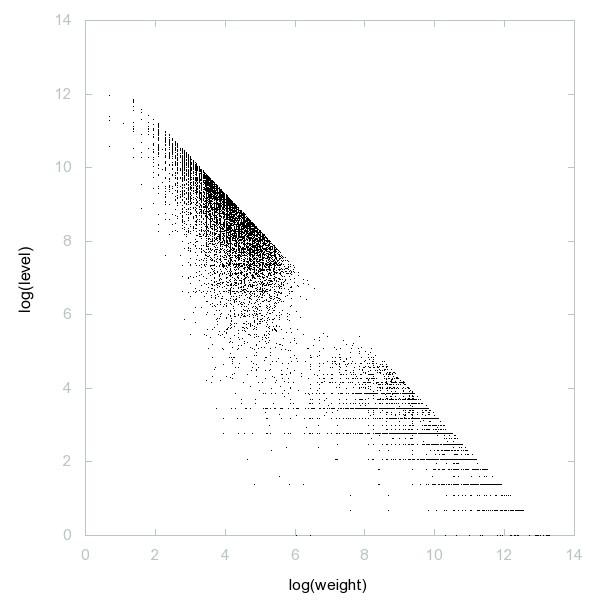
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of 8-almost primes

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers that are divisible by exactly 8 primes counting multiplicity.
A046310(n) = A000000(n) * A000000(n) + A114408(n)
Download CSV of the decomposition of 8-almost primes (9999 lines.)
Decomposition of 8-almost primes - 9997 dots.

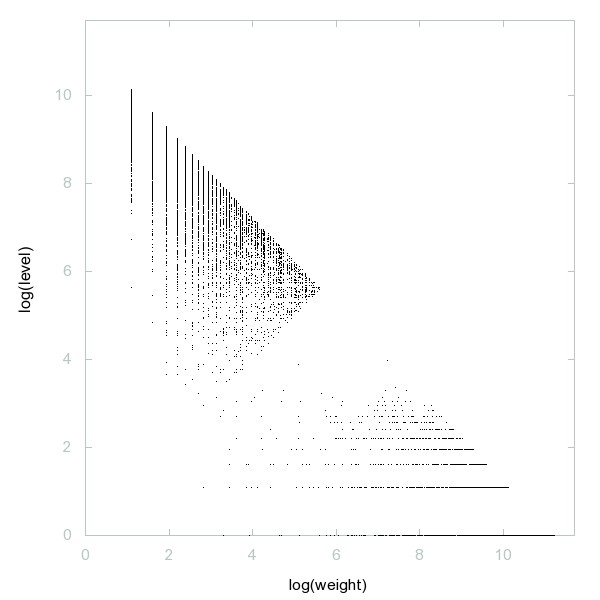
Decomposition of A046316

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Odd numbers divisible by exactly 3 primes (counted with multiplicity).
A046316(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A046316 (9999 lines.)
Decomposition of A046316 - 9998 dots.

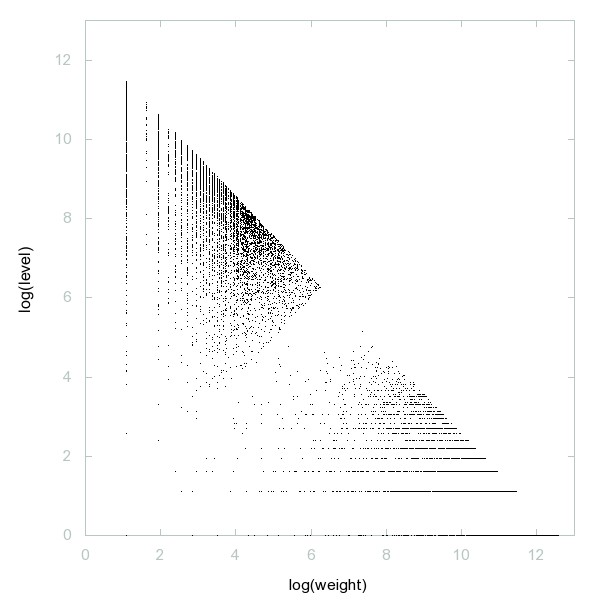
Decomposition of A046386

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Products of four distinct primes.
A046386(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A046386 (9999 lines.)
Decomposition of A046386 - 9998 dots.

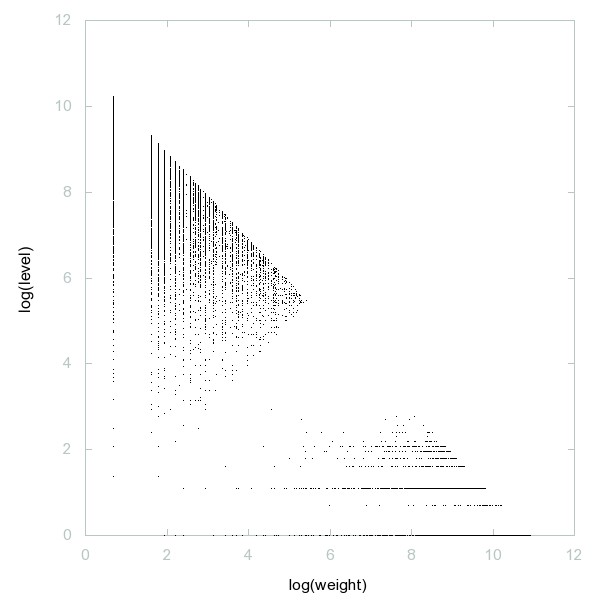
Decomposition of A046411

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Concatenation of prime factors of a(n) is a prime.
A046411(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A046411 (9999 lines.)
Decomposition of A046411 - 9997 dots.

Decomposition of A046642

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that n and number of divisors d(n) are relatively prime.
A046642(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A046642 (9999 lines.)
Decomposition of A046642 - 9997 dots.

Decomposition of Additive primes

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Additive primes: sum of digits is a prime.
A046704(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of Additive primes (9999 lines.)
Decomposition of Additive primes - 9995 dots.

Decomposition of A046711

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
From the Bruck-Ryser theorem: n == 1 or 2 (mod 4) which are also the sum of 2 squares.
A046711(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A046711 (9999 lines.)
Decomposition of A046711 - 9996 dots.

Decomposition of A046712

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
From the Bruck-Ryser theorem: n == 1 or 2 (mod 4) which are not the sum of 2 squares.
A046712(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A046712 (9999 lines.)
Decomposition of A046712 - 9997 dots.

Decomposition of Equidigital numbers

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Equidigital numbers.
A046758(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of Equidigital numbers (9999 lines.)
Decomposition of Equidigital numbers - 9996 dots.

Decomposition of Economical numbers

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Economical numbers: write n as a product of primes raised to powers, let D(n) = number of digits in product, l(n) = number of digits in n; sequence gives n such that D(n)<l(n).
A046759(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of Economical numbers (9999 lines.)
Decomposition of Economical numbers - 9998 dots.