Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of Oddish numbers

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Oddish numbers (prime to 10 and 10's digit is odd).
A045798(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of Oddish numbers (9999 lines.)
Decomposition of Oddish numbers - 9998 dots.

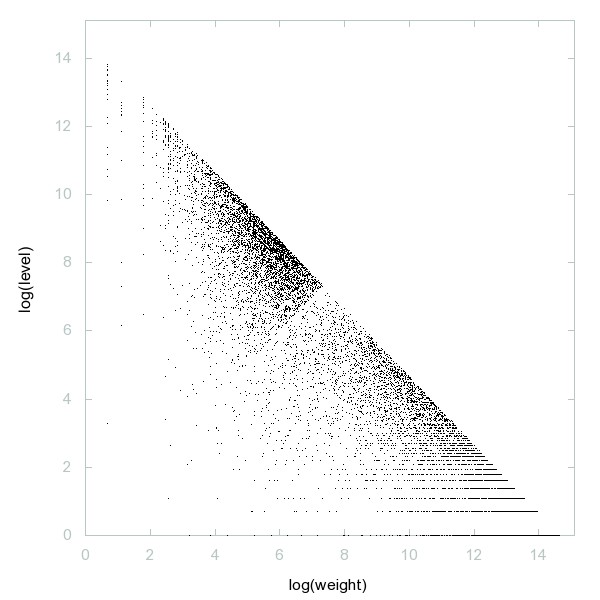
Decomposition of A045844

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
a(n+1) = a(n) + largest digit of a(n); a(0) = 1.
A045844(n) = A000000(n) * A000000(n) + A132137(n+1)
Download CSV of the decomposition of A045844 (10000 lines.)
Decomposition of A045844 - 9996 dots.

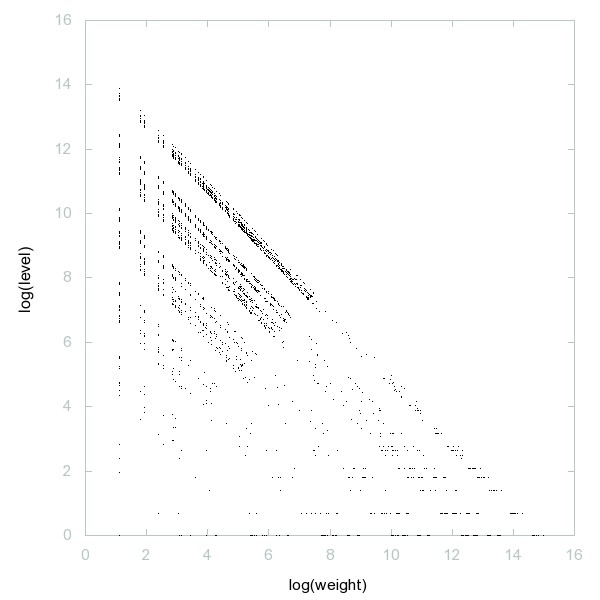
Decomposition of A045920

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that factorizations of n and n+1 have same number of primes (including multiplicities).
A045920(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A045920 (9999 lines.)
Decomposition of A045920 - 9996 dots.

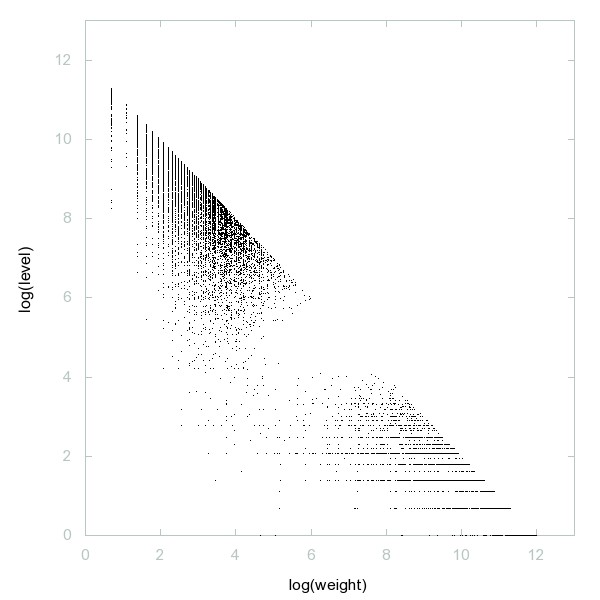
Decomposition of A045939

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that factorizations of n through n+2 have the same number of primes (including multiplicities).
A045939(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A045939 (9999 lines.)
Decomposition of A045939 - 9998 dots.

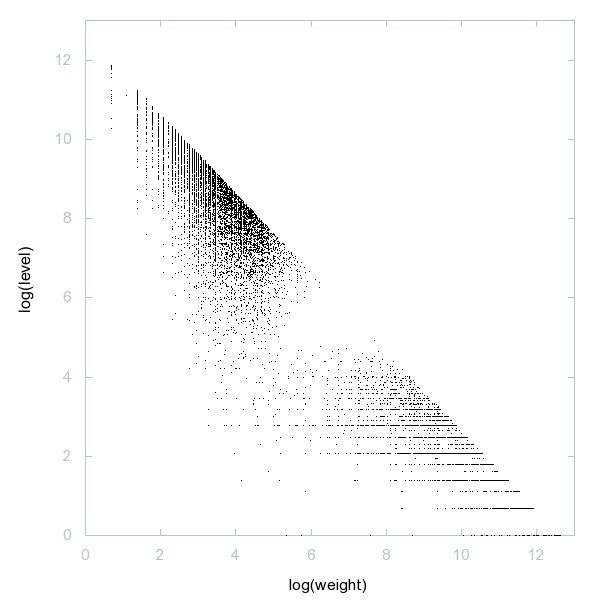
Decomposition of A045941

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that the factorizations of n through n+4 have the same number of primes (including multiplicities).
A045941(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A045941 (9999 lines.)
Decomposition of A045941 - 9995 dots.

Decomposition of A045942

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that the factorizations of n through n+5 have the same number of primes (including multiplicities).
A045942(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A045942 (9999 lines.)
Decomposition of A045942 - 9996 dots.

Decomposition of A046025

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that 6n+1, 12n+1 and 18n+1 are all primes.
A046025(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A046025 (9999 lines.)
Decomposition of A046025 - 9995 dots.

Decomposition of A046034

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers whose digits are primes.
A046034(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A046034 (9999 lines.)
Decomposition of A046034 - 9991 dots.

Decomposition of 6-almost primes

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers that are divisible by exactly 6 primes with multiplicity.
A046306(n) = A000000(n) * A000000(n) + A114406(n)
Download CSV of the decomposition of 6-almost primes (9999 lines.)
Decomposition of 6-almost primes - 9997 dots.

Decomposition of 7-almost primes

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers that are divisible by exactly 7 primes counting multiplicity.
A046308(n) = A000000(n) * A000000(n) + A114407(n)
Download CSV of the decomposition of 7-almost primes (9999 lines.)
Decomposition of 7-almost primes - 9997 dots.