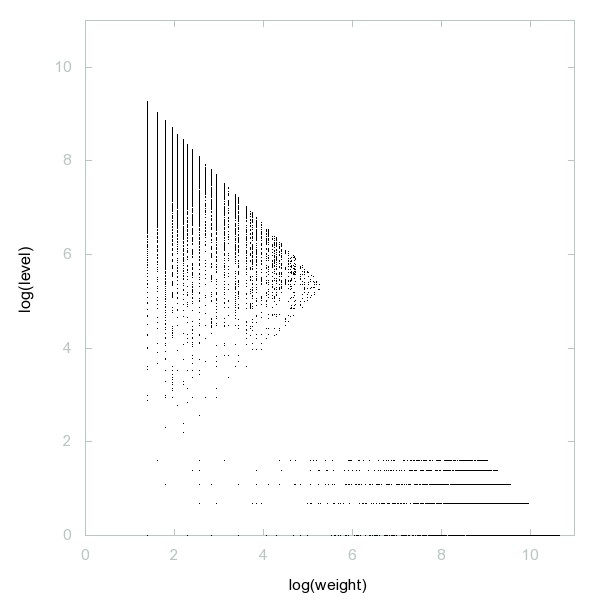
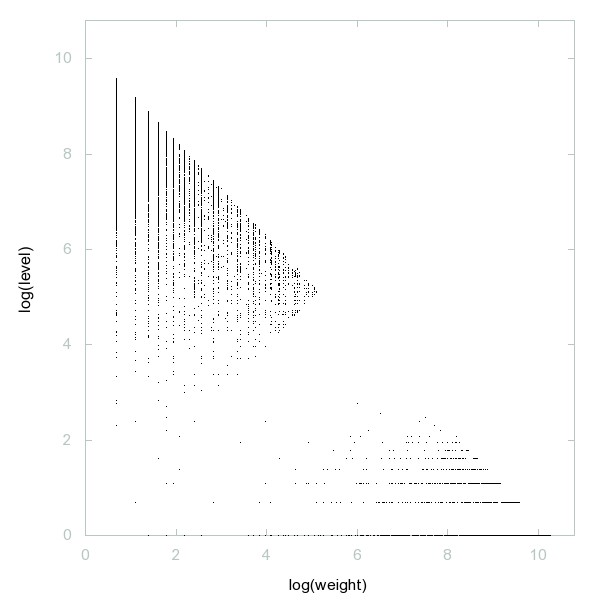
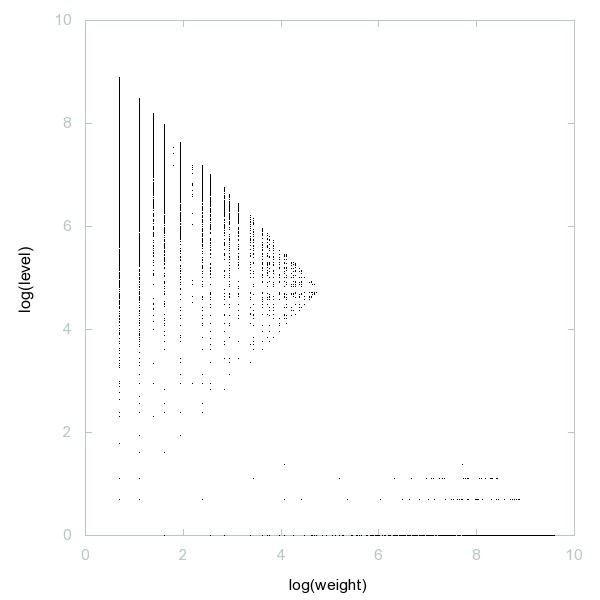
Decomposition of A035333
Concatenation of two or more consecutive positive integers.
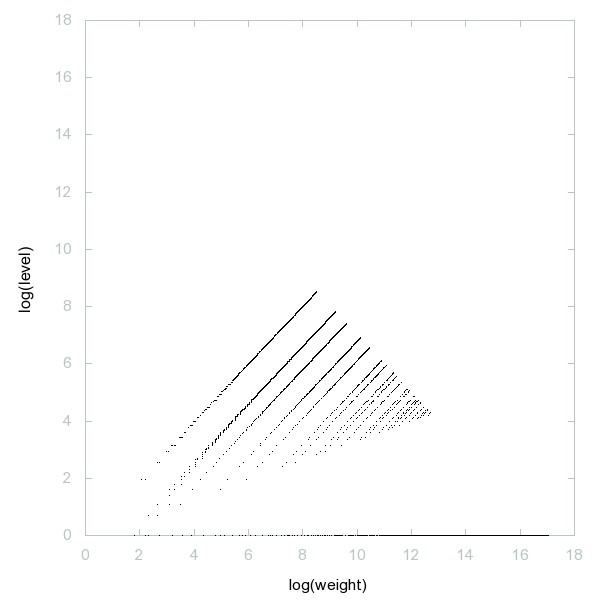
Decomposition of A035336
a(n) = 2*floor(n*phi) + n - 1, where phi = (1+sqrt(5))/2.
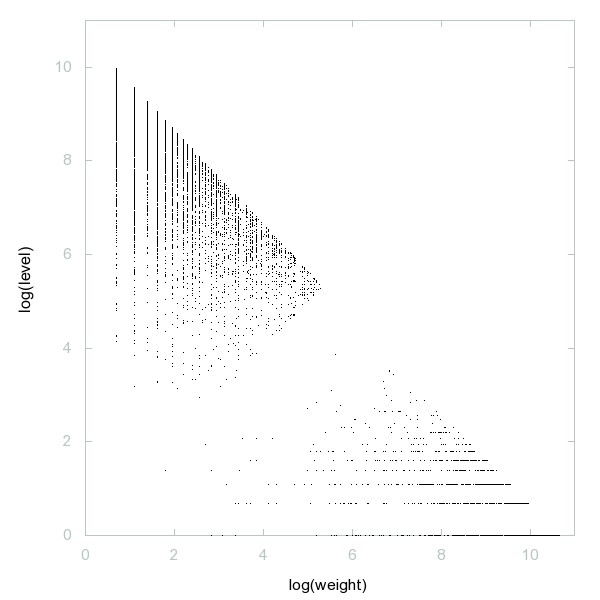
Decomposition of Happy primes
Happy primes: primes that eventually reach 1 under iteration of "x -> sum of squares of digits of x".
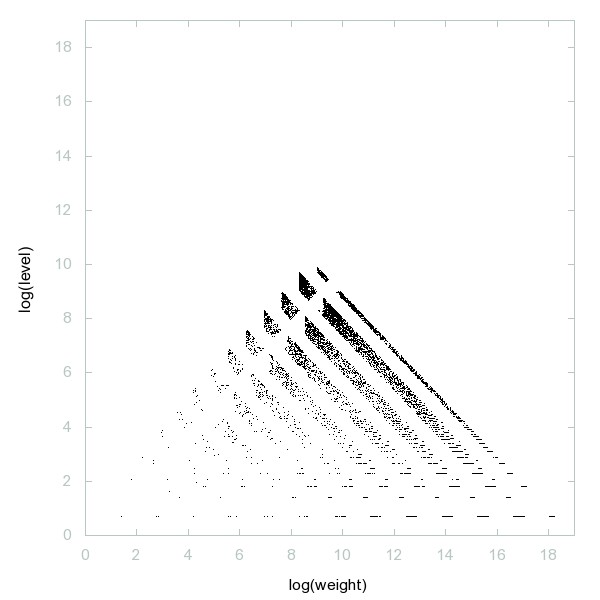
Decomposition of A035928
Numbers n such that BCR(n) = n, where BCR = binary-complement-and-reverse = take one's complement then reverse bit order.
Decomposition of A036301
Numbers n such that sum of even digits of n equals sum of odd digits of n.
Decomposition of A036433
Number of divisors is a digit in the base 10 representation of n.
Decomposition of A036441
a(n+1) = next number having largest prime dividing a(n) as a factor, with a(1) = 2.
Decomposition of A036455
Numbers n such that d(d(n)) is an odd prime, where d(k) is the number of divisors of k.
Decomposition of A036537
Numbers n such that number of divisors of n is a power of 2.
Decomposition of A036990
Numbers n such that, in the binary expansion of n, reading from right to left, the number of 1's never exceeds the number of 0's.