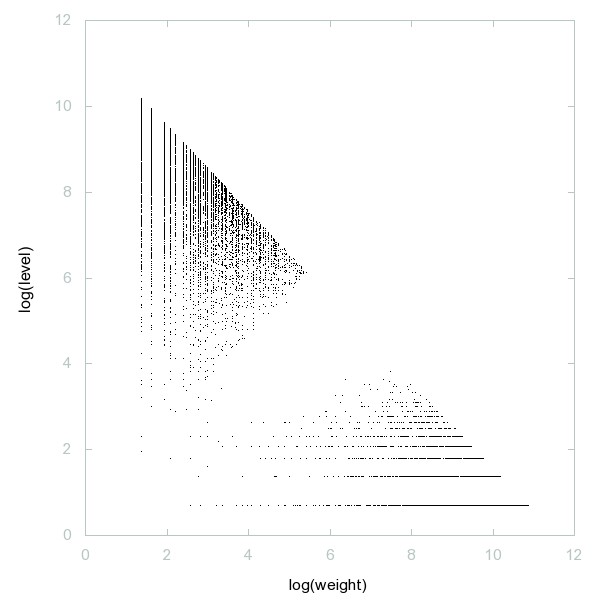
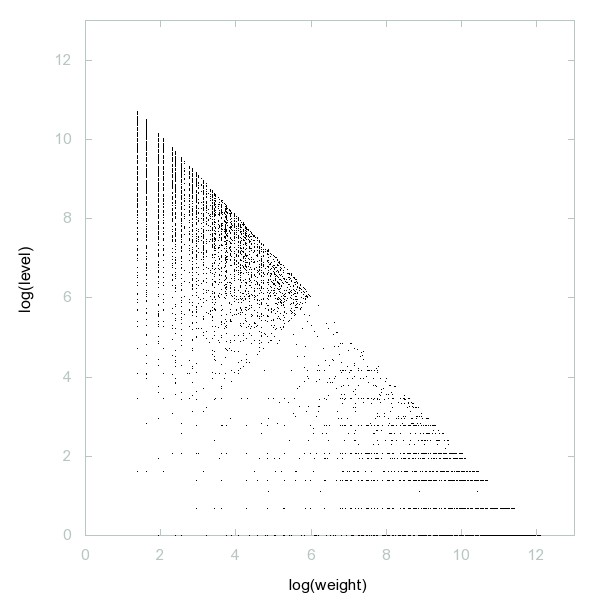
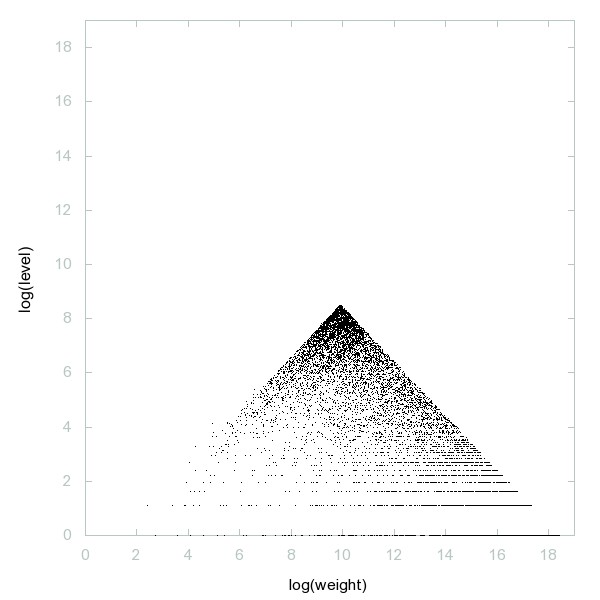
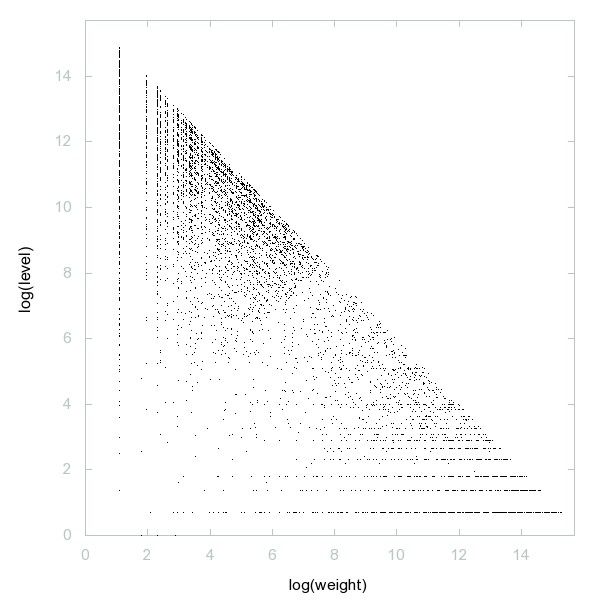
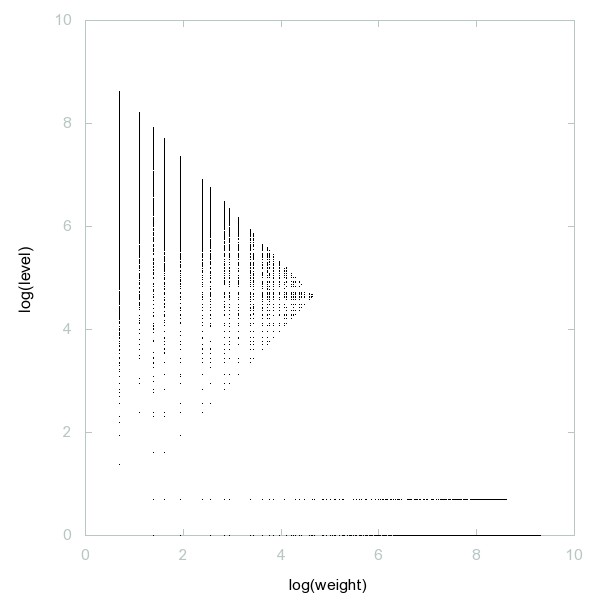
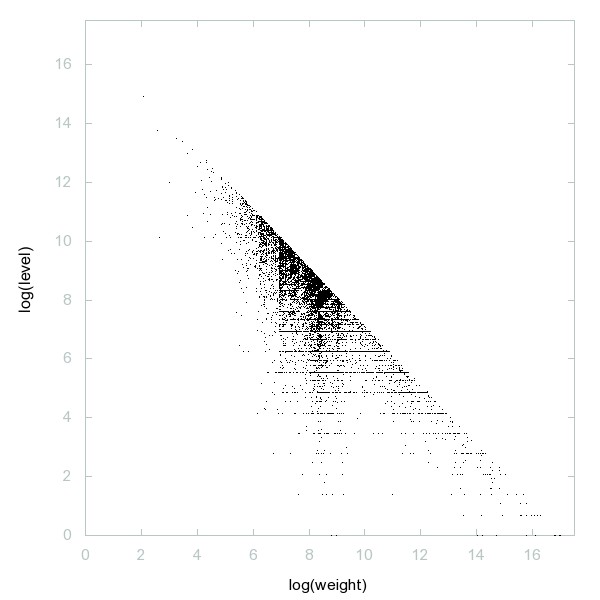
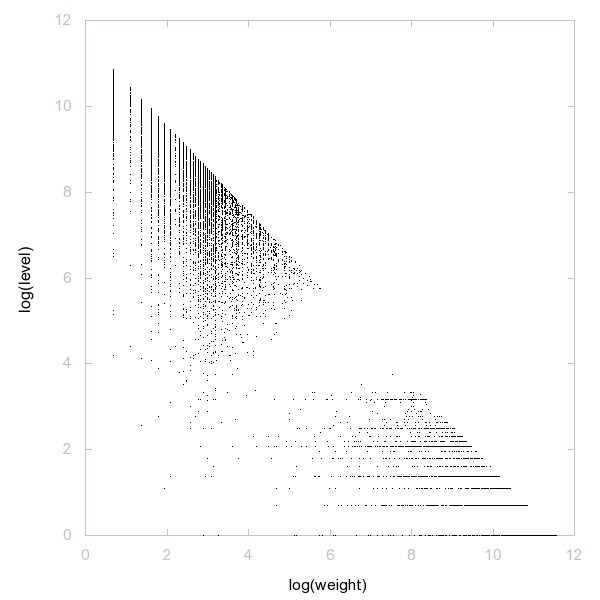
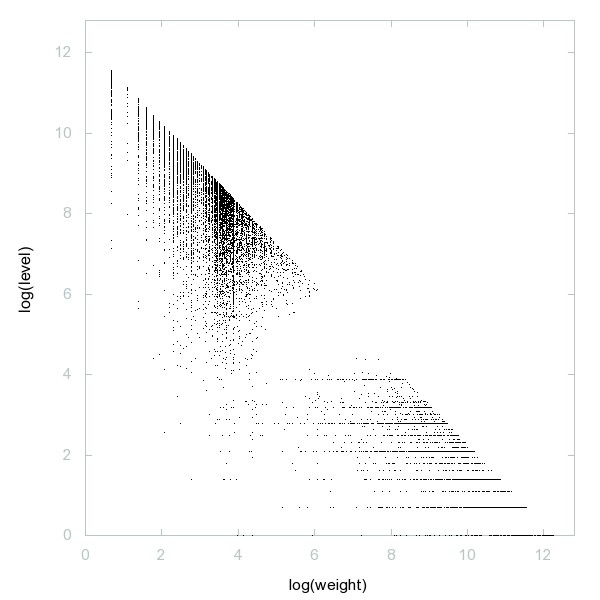
Decomposition of Fouvry-Iwaniec primes
Fouvry-Iwaniec primes: Primes of the form k^2 + p^2 where p is a prime.
Decomposition of A187813
Numbers n whose base-b digit sum is not b for all bases b >= 2.
Decomposition of A190803
Increasing sequence generated by these rules: a(1)=1, and if x is in a then 2x-1 and 3x-1 are in a.
Decomposition of A190898
Least odd prime p>n^2 with (n/p) = 1, where (-) is the Legendre symbol
Decomposition of A191113
Increasing sequence generated by these rules: a(1)=1, and if x is in a then 3x-2 and 4x-2 are in a.
Decomposition of Nonludic numbers
Nonludic numbers: complement of A003309.
Decomposition of A195069
Numbers n such that (number of integer factors of n counted with multiplicity) less (number of distinct integer factors of n) = 10.
Decomposition of A195086
Numbers n such that (number of prime factors of n counted with multiplicity) less (number of distinct prime factors of n) = 2.
Decomposition of A195087
Numbers n such that (number of prime factors of n counted with multiplicity) less (number of distinct prime factors of n) = 3.
Decomposition of A195270
3-gap primes: Prime p is a term iff there is no prime between 3*p and 3*q, where q is the next prime after p.