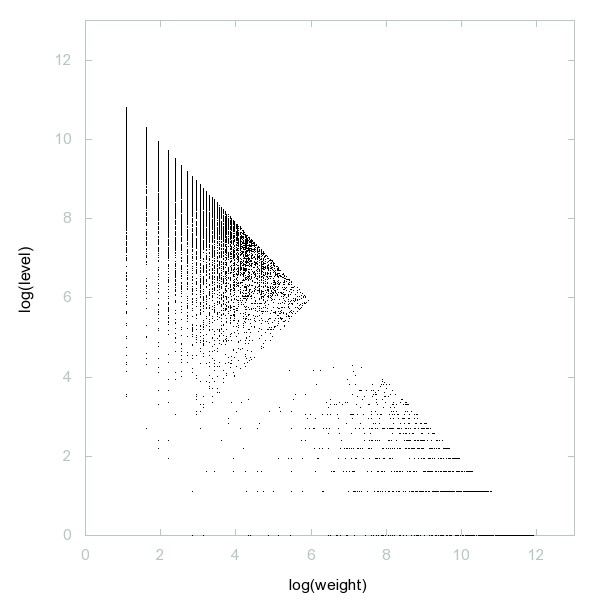
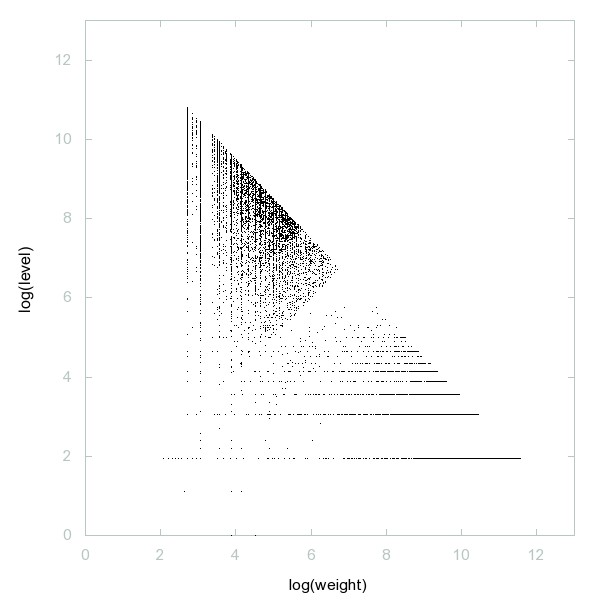
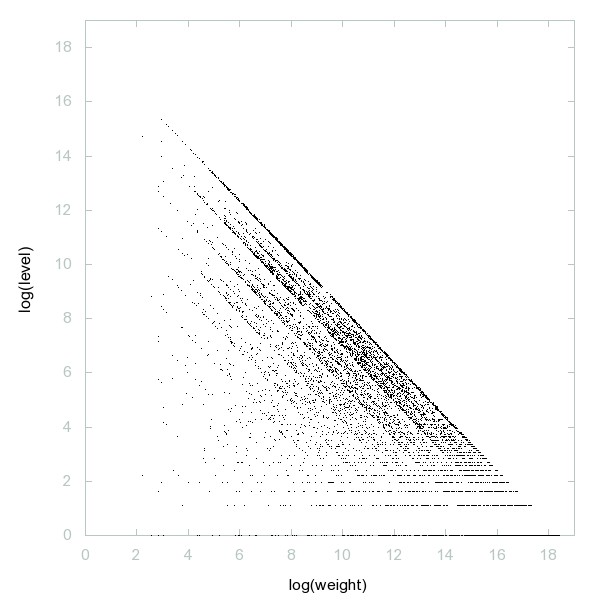
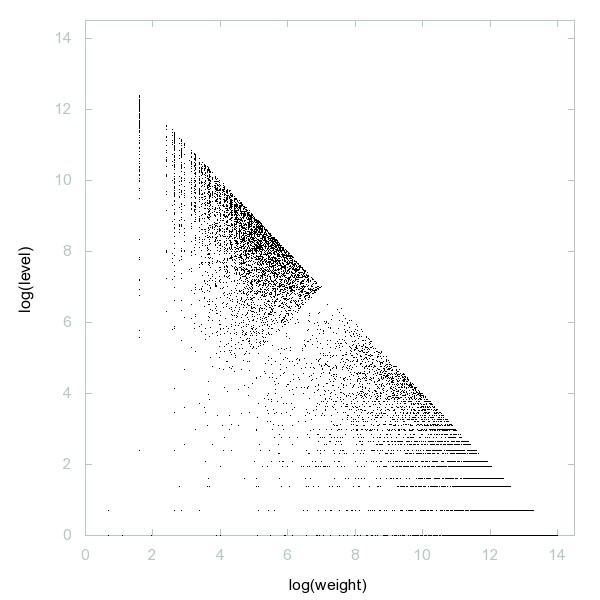
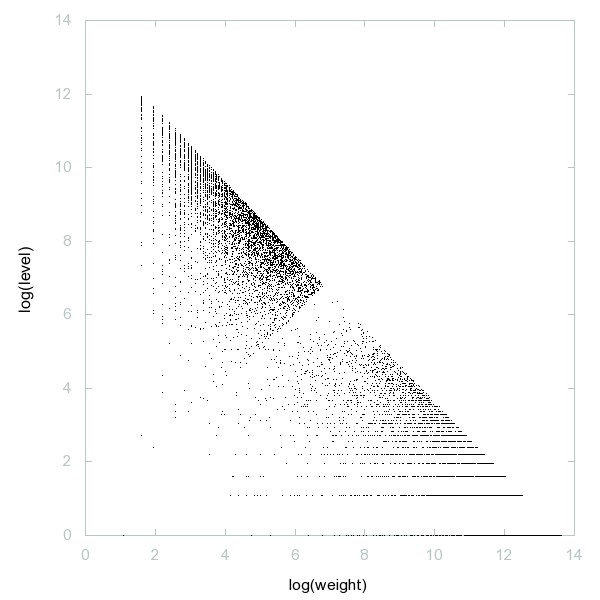
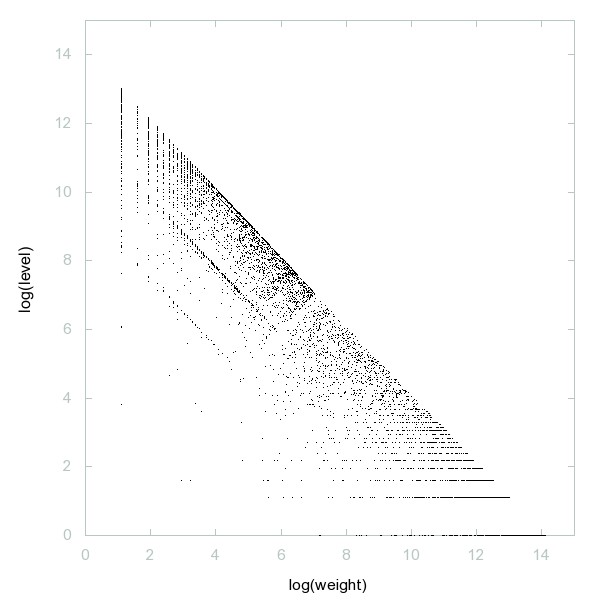
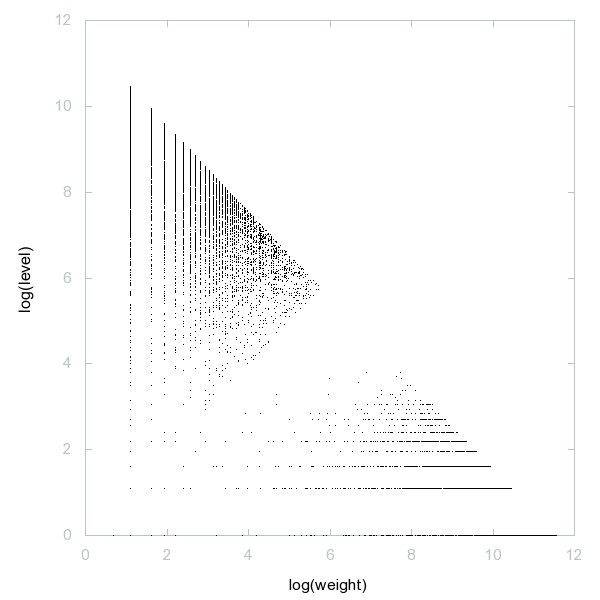
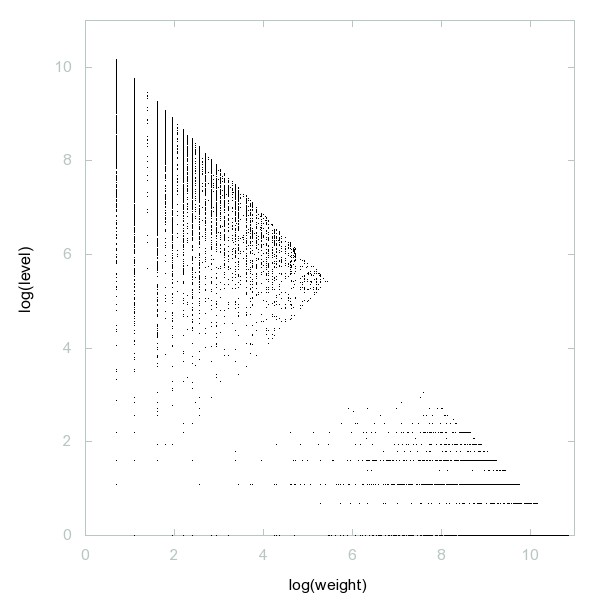
Decomposition of Primes classified by weight
Primes classified by weight.
Decomposition of A162527
Numbers n such that their largest divisor <= sqrt(n) equals 7.
Decomposition of A162795
Total number of toothpicks in the toothpick structure A139250 that are parallel to the initial toothpick, after n odd rounds.
Decomposition of A162862
Numbers n such that n^10+n^9+n^8+n^7+n^6+n^5+n^4+n^3+n^2+n+1 is prime.
Decomposition of A164977
Numbers m such that the set {1..m} has only one nontrivial decomposition into subsets with equal element sum.
Decomposition of Isolated primes
Isolated primes: Primes p such that there is no other prime in the interval [2*prevprime(p/2), 2*nextprime(p/2)].
Decomposition of A166573
Prime numbers containing the string 13.
Decomposition of A166684
Numbers n such that d(n)<4.
Decomposition of Orderly numbers
Orderly numbers: a number n is orderly if there exists some number k > tau(n) such that the set of the divisors of n is congruent to the set {1,2,...,tau(n)} mod k.
Decomposition of Single numbers
The single or isolated numbers. The union of single (or isolated or non-twin) primes and single (or isolated or average of twin prime pairs) nonprimes.