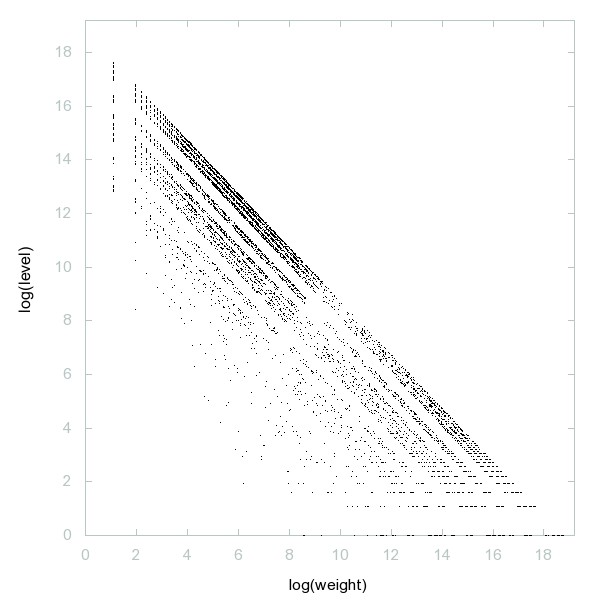
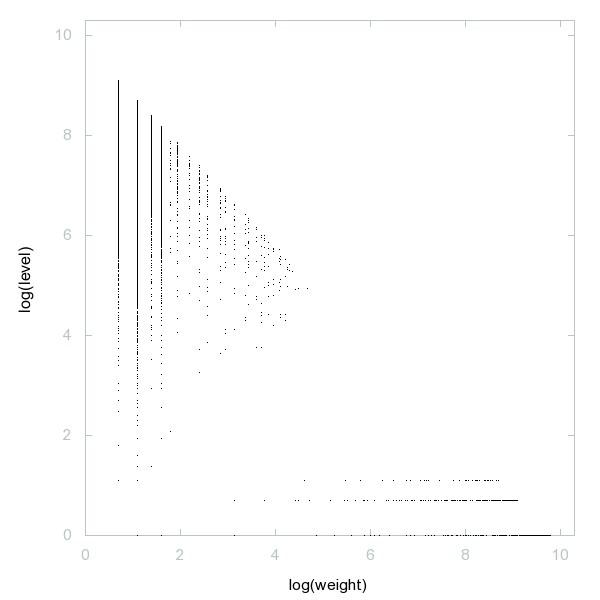
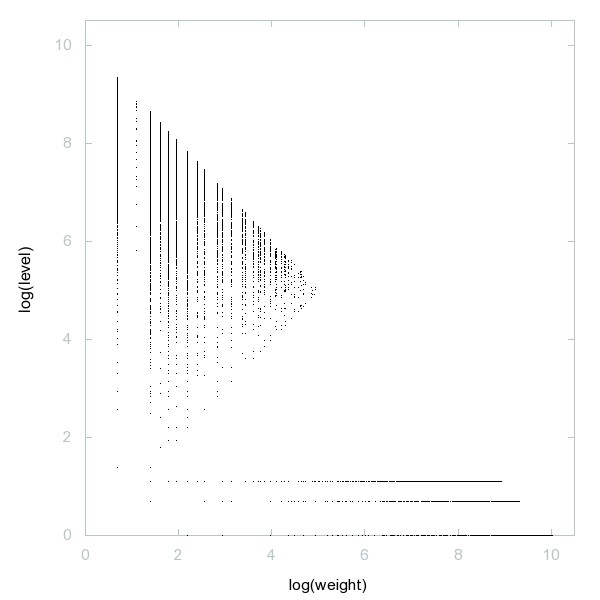
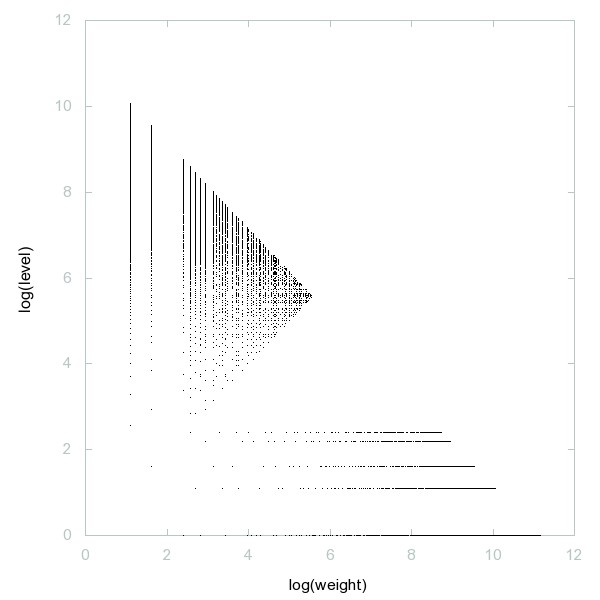
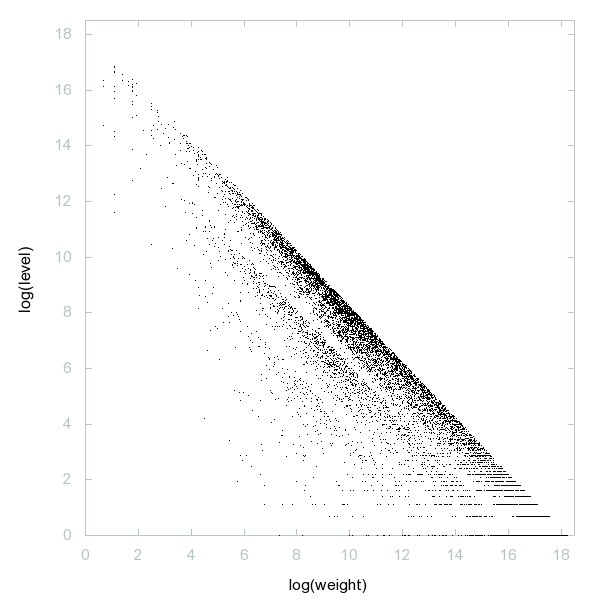
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of A108386

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes p such that p's set of distinct digits is {1,3,7,9}.
A108386(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A108386 (9999 lines.)
Decomposition of A108386 - 9989 dots.

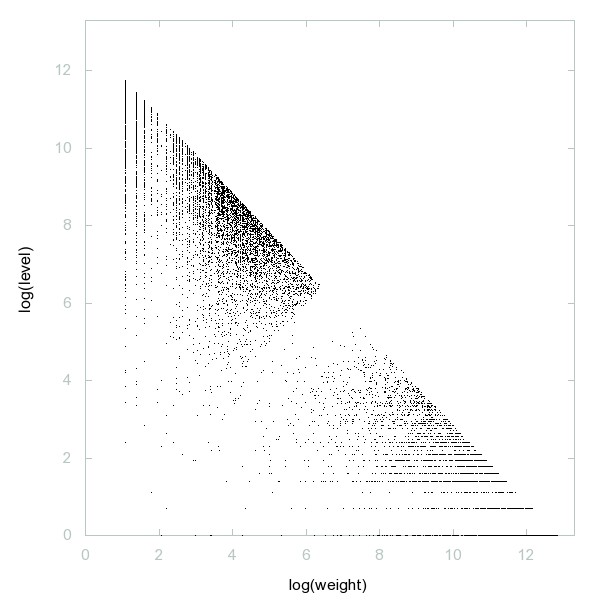
Decomposition of A109303

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n with at least one duplicate base 10 digit (A107846(n) > 0).
A109303(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A109303 (9999 lines.)
Decomposition of A109303 - 9997 dots.

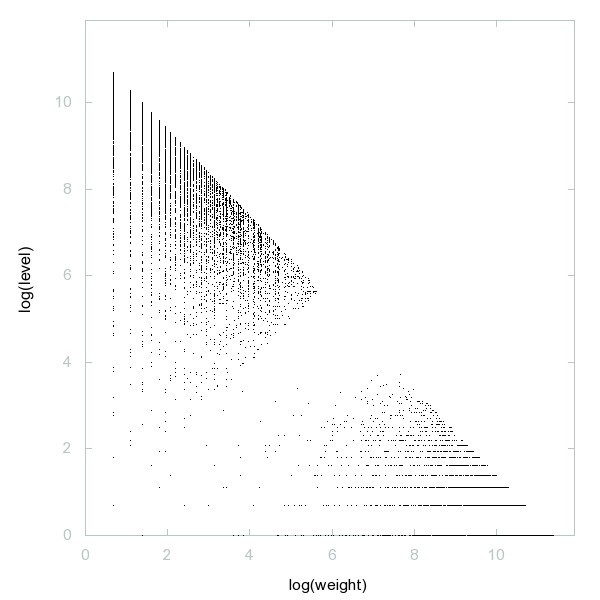
Decomposition of A109373

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Semiprimes of the form semiprime + 1.
A109373(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A109373 (9999 lines.)
Decomposition of A109373 - 9998 dots.

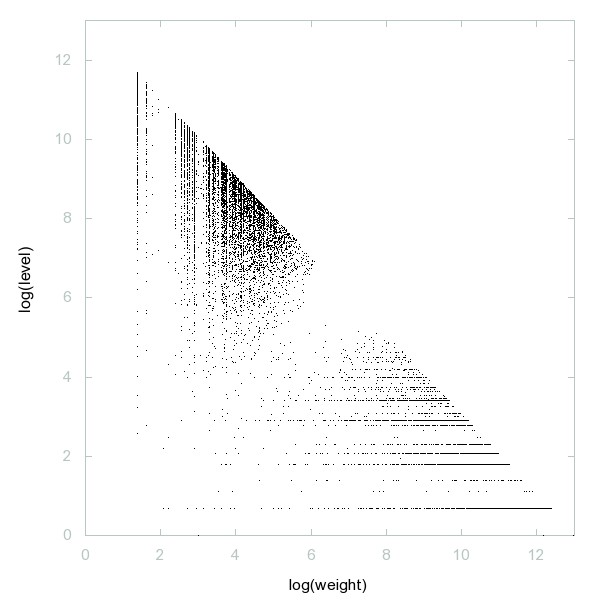
Decomposition of A111046

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Difference between squares of twin prime pairs.
A111046(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A111046 (9999 lines.)
Decomposition of A111046 - 9995 dots.

Decomposition of A111501

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that n^3 - n^2 + 1 is prime.
A111501(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A111501 (9999 lines.)
Decomposition of A111501 - 9995 dots.

Decomposition of Admirable numbers

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Admirable numbers. A number n is admirable if there exists a proper divisor d' of n such that sigma(n)-2d'=2n, where sigma(n) is the sum of all divisors of n.
A111592(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of Admirable numbers (9999 lines.)
Decomposition of Admirable numbers - 9998 dots.

Decomposition of A112886

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Triangle-free positive integers.
A112886(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A112886 (9999 lines.)
Decomposition of A112886 - 9997 dots.

Decomposition of A113502

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
A number n is included if at least one of its divisors > 1 is a triangular number (i.e., is of the form m(m+1)/2, m >= 2).
A113502(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A113502 (9999 lines.)
Decomposition of A113502 - 9997 dots.

Decomposition of A113801

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers that are congruent to {1, 13} mod 14.
A113801(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A113801 (9999 lines.)
Decomposition of A113801 - 9997 dots.

Decomposition of A115921

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that the decimal digits of phi(n) are a permutation of those of n.
A115921(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A115921 (9999 lines.)
Decomposition of A115921 - 9993 dots.