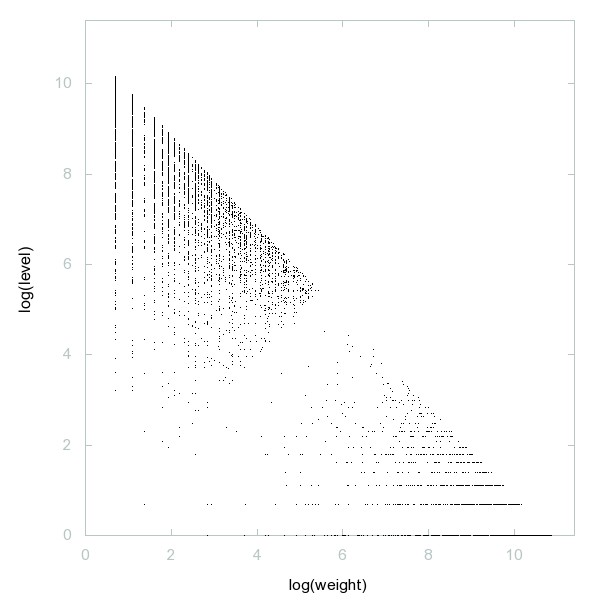
Decomposition of A090050
Numbers having equal length of longest contiguous block of zeros and ones in binary expansion.
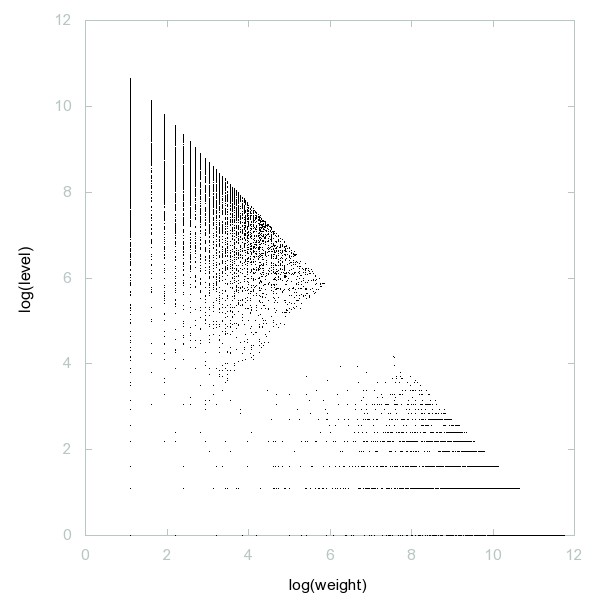
Decomposition of Symmetric primes
Symmetric primes: an odd prime p is symmetric if there exists an odd prime q such that |p-q|=gcd(p-1,q-1).
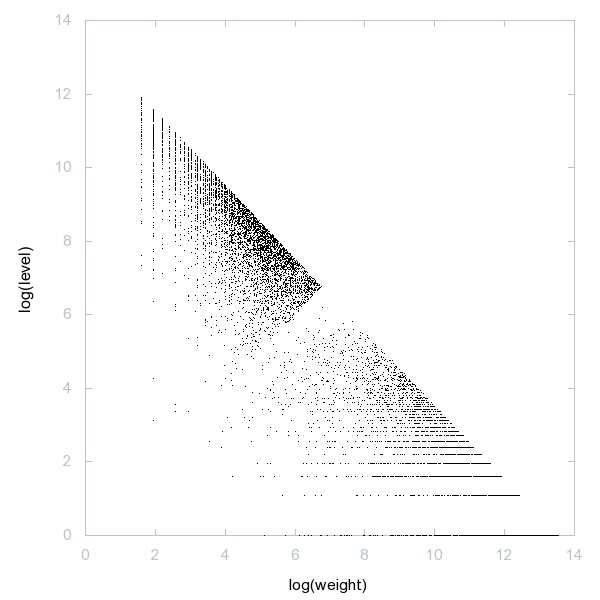
Decomposition of Asymmetric primes
Asymmetric primes: an odd prime p is asymmetric if there is no odd prime q such that |p-q|=gcd(p-1,q-1).
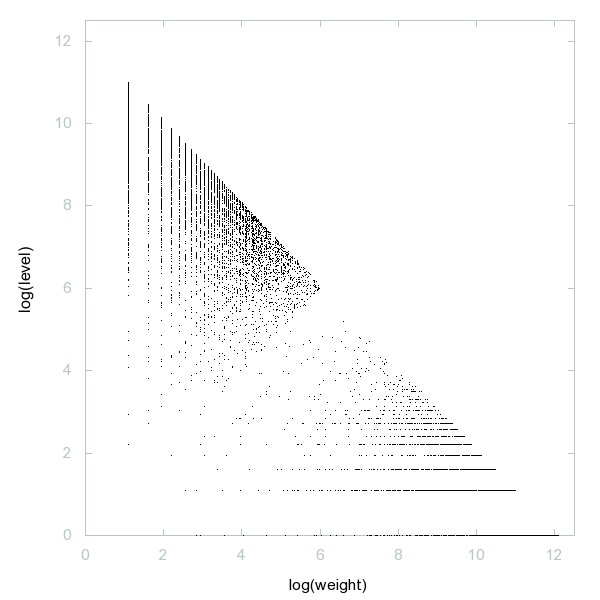
Decomposition of A090403
Balanced primes: Primes which are both the arithmetic mean and median of a sequence of 2k+1 consecutive primes, for some k>0.
Decomposition of A090421
Numbers that can be written in binary representation as concatenation of primes.
Decomposition of A090423
Primes that can be written in binary representation as concatenation of other primes.
Decomposition of A090466
Regular figurative or polygonal numbers of order greater than 2.
Decomposition of A090693
Positive numbers n such that n^2 - 2n + 2 is a prime.
Decomposition of A090709
Primes whose decimal representation is a valid number in base 6 and interpreted as such is again a prime.
Decomposition of A090771
Numbers that are congruent to {1, 9} mod 10.