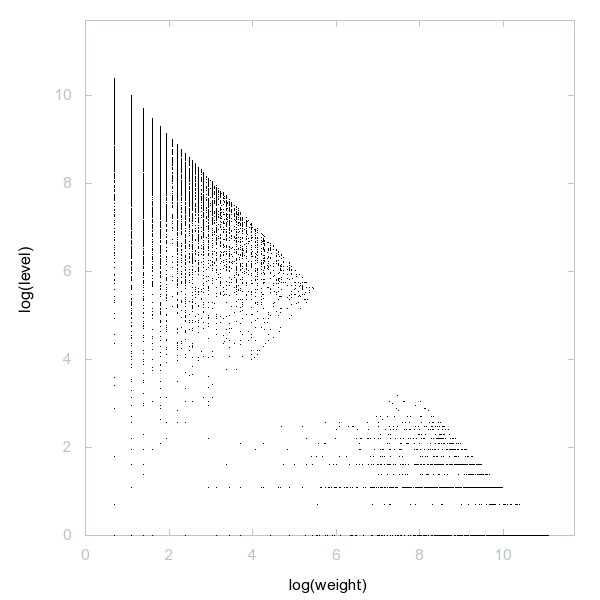
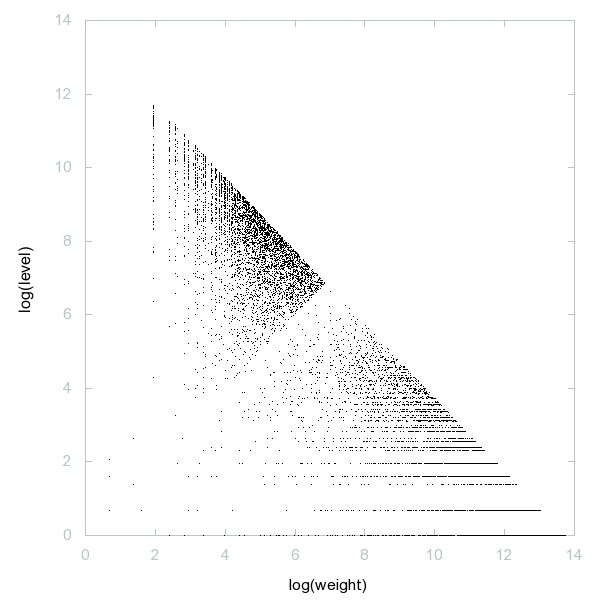
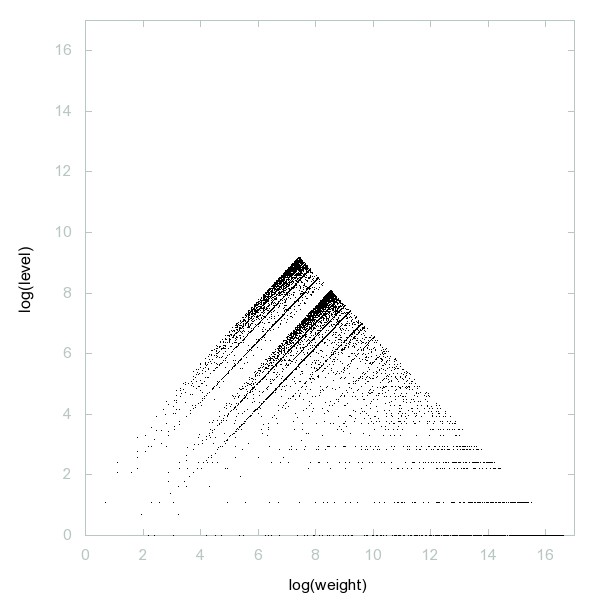
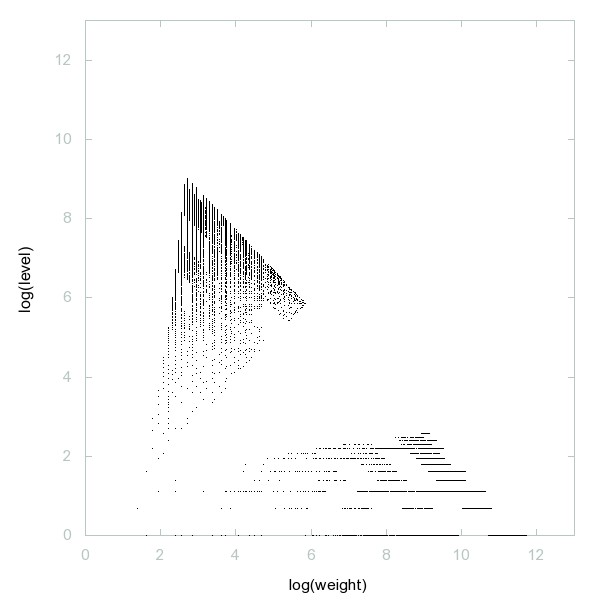
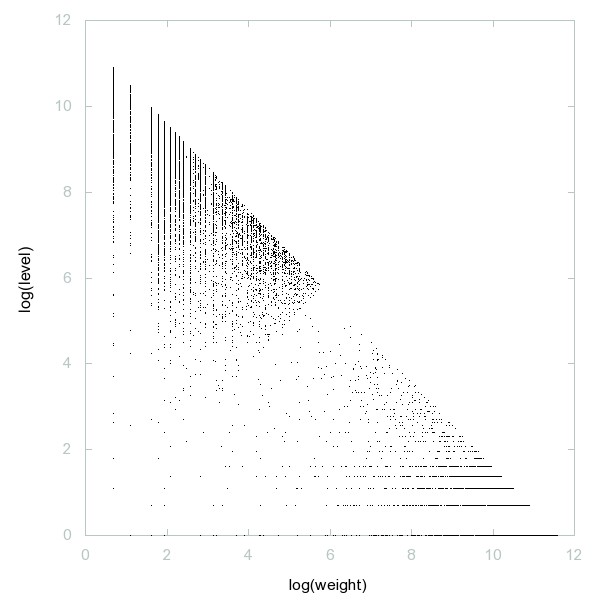
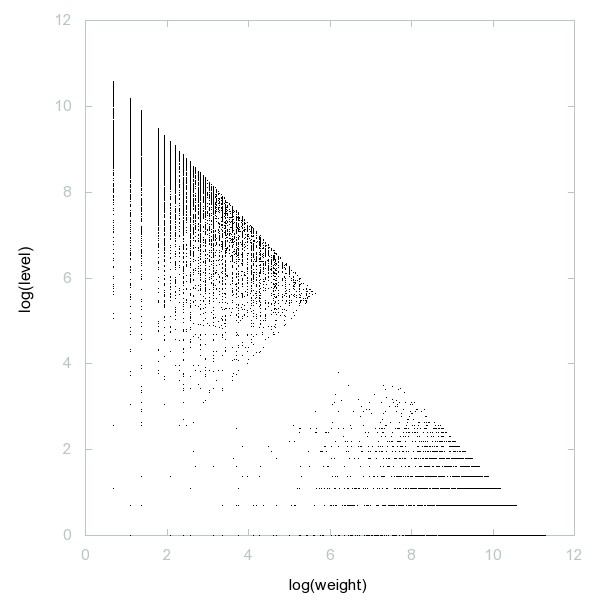
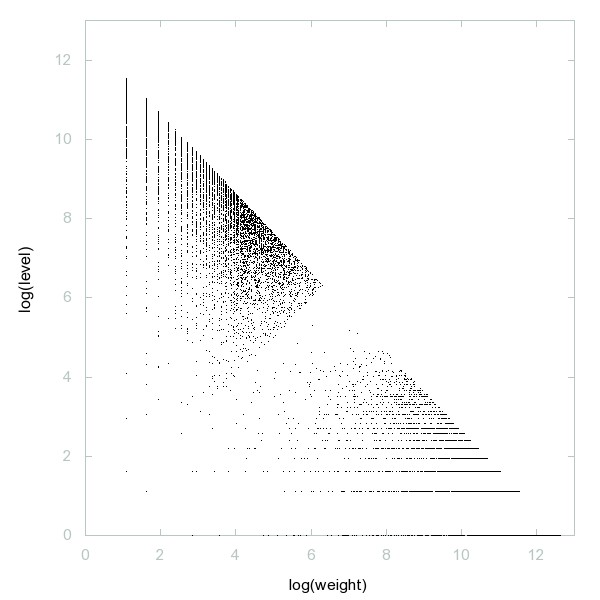
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of A001751

3D graph (WebGL) / 2D graph - First 500 terms
Primes together with primes multiplied by 2.
A001751(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A001751 (9999 lines.)
Decomposition of A001751 - 9998 dots.

Decomposition of A001838

3D graph (WebGL) / 2D graph - First 500 terms
Numbers n such that phi(n+2) = phi(n) + 2.
A001838(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A001838 (9999 lines.)
Decomposition of A001838 - 9997 dots.

Decomposition of A001839

3D graph (WebGL) / 2D graph - First 500 terms
The coding-theoretic function A(n,4,3).
A001839(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A001839 (9996 lines.)
Decomposition of A001839 - 9992 dots.

Decomposition of Sorting numbers

3D graph (WebGL) / 2D graph - First 500 terms
Sorting numbers: maximal number of comparisons for sorting n elements by binary insertion.
A001855(n) = A000000(n) * A000000(n) + A029837(n)
Download CSV of the decomposition of Sorting numbers (10000 lines.)
Decomposition of Sorting numbers - 9996 dots.

Decomposition of A001857

3D graph (WebGL) / 2D graph - First 500 terms
a(1)=2, a(2)=3; for n >= 3, a(n) is smallest number which is uniquely of the form a(j)+a(k) with 1<=j<k<n.
A001857(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A001857 (9999 lines.)
Decomposition of A001857 - 9997 dots.

Decomposition of A001912

3D graph (WebGL) / 2D graph - First 500 terms
Numbers n such that 4*n^2 + 1 is prime.
A001912(n) = A000000(n) * A000000(n) + A214517(n)
Download CSV of the decomposition of A001912 (9999 lines.)
Decomposition of A001912 - 9996 dots.

Decomposition of Full reptend primes

3D graph (WebGL) / 2D graph - First 500 terms
Full reptend primes: primes with primitive root 10.
A001913(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of Full reptend primes (9999 lines.)
Decomposition of Full reptend primes - 9996 dots.

Decomposition of A001952

3D graph (WebGL) / 2D graph - First 500 terms
A Beatty sequence: a(n) = floor(n*(2 + sqrt(2))).
A001952(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A001952 (9999 lines.)
Decomposition of A001952 - 9997 dots.

Decomposition of Evil numbers

3D graph (WebGL) / 2D graph - First 500 terms
Evil numbers: numbers with an even number of 1's in their binary expansion.
A001969(n) = A000000(n) * A000000(n) + A036585(n)
Download CSV of the decomposition of Evil numbers (9999 lines.)
Decomposition of Evil numbers - 9996 dots.

Decomposition of Segmented numbers

3D graph (WebGL) / 2D graph - First 500 terms
Segmented numbers, or prime numbers of measurement.
A002048(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of Segmented numbers (7835 lines.)
Decomposition of Segmented numbers - 7832 dots.