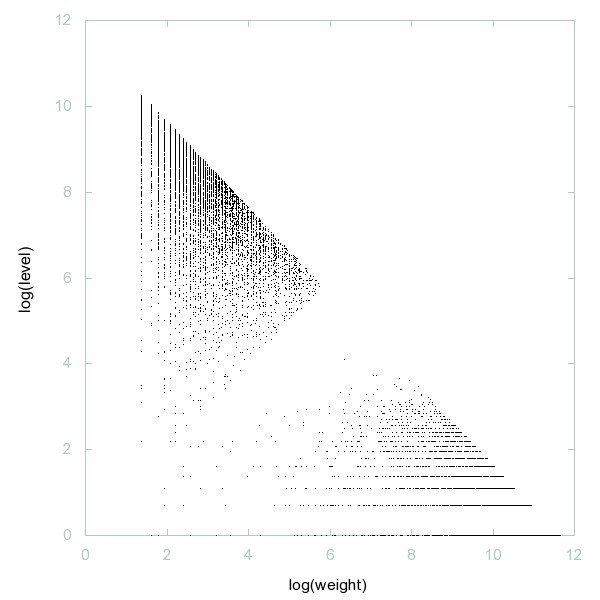
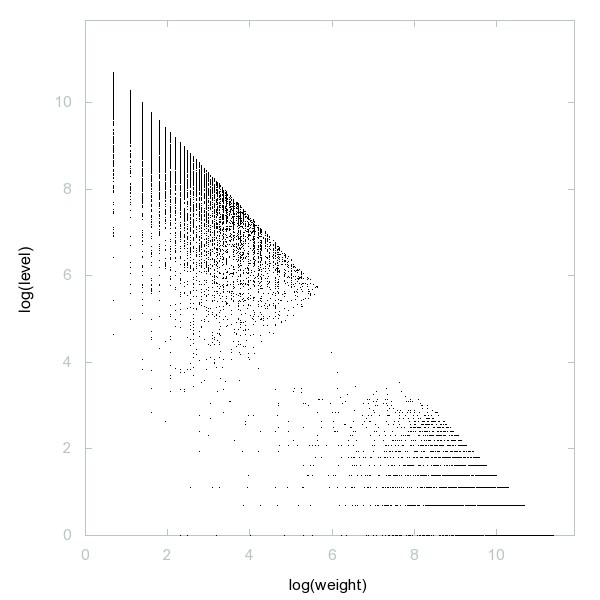
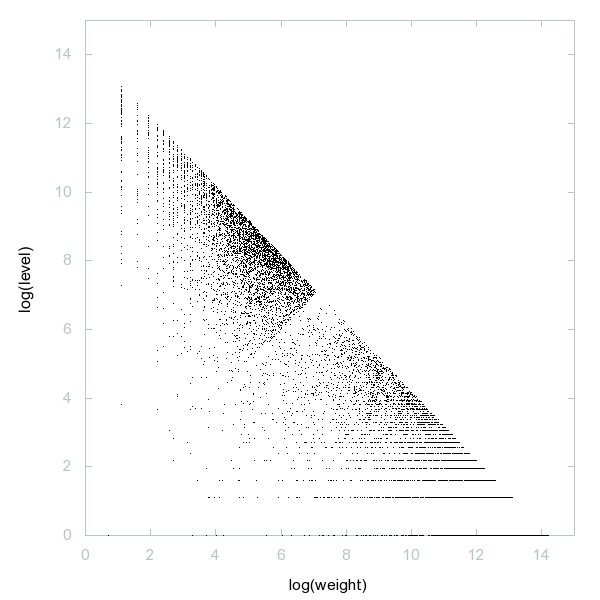
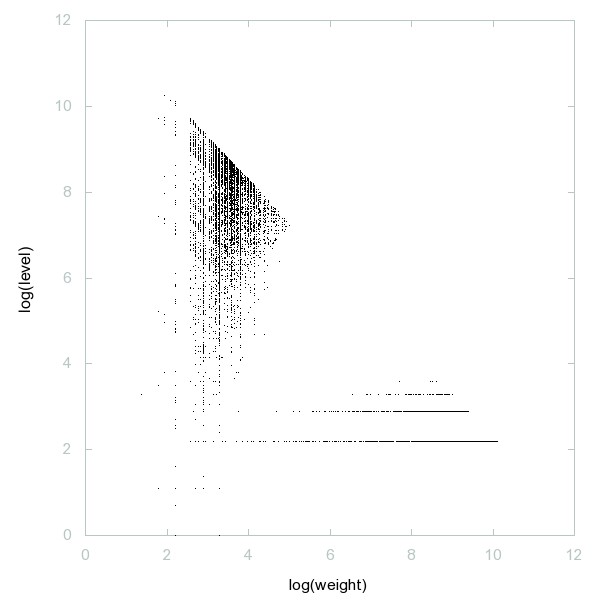
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of 5-almost primes

3D graph (WebGL) / 2D graph - First 500 terms
Numbers that are products of 5 primes (or 5-almost primes, a generalization of semiprimes).
A014614(n) = A000000(n) * A000000(n) + A114405(n)
Download CSV of the decomposition of 5-almost primes (9999 lines.)
Decomposition of 5-almost primes - 9997 dots.

Decomposition of A014688

3D graph (WebGL) / 2D graph - First 500 terms
a(n) = n-th prime + n.
A014688(n) = A000000(n) * A000000(n) + A001223(n) + 1
Download CSV of the decomposition of A014688 (9999 lines.)
Decomposition of A014688 - 9997 dots.

Decomposition of A014847

3D graph (WebGL) / 2D graph - First 500 terms
Numbers n such that n-th Catalan number C(2n,n)/(n+1) is divisible by n.
A014847(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A014847 (9999 lines.)
Decomposition of A014847 - 9995 dots.

Decomposition of A015614

3D graph (WebGL) / 2D graph - First 500 terms
Sum( phi(i), i=1..n) - 1.
A015614(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A015614 (9999 lines.)
Decomposition of A015614 - 9994 dots.

Decomposition of A015911

3D graph (WebGL) / 2D graph - First 500 terms
Numbers n such that 2^n mod n is odd.
A015911(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A015911 (9999 lines.)
Decomposition of A015911 - 9997 dots.

Decomposition of A016038

3D graph (WebGL) / 2D graph - First 500 terms
Strictly non-palindromic numbers: n is not palindromic in any base b with 2 <= b <= n-2.
A016038(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A016038 (10000 lines.)
Decomposition of A016038 - 9993 dots.

Decomposition of A016052

3D graph (WebGL) / 2D graph - First 500 terms
a(1) = 3; for n >= 1, a(n+1) = a(n) + sum of its digits.
A016052(n) = A000000(n) * A000000(n) + A084228(n+2)
Download CSV of the decomposition of A016052 (9999 lines.)
Decomposition of A016052 - 9997 dots.

Decomposition of A016096

3D graph (WebGL) / 2D graph - First 500 terms
a(n+1) = a(n) + sum of its digits, with a(1) = 9.
A016096(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A016096 (9999 lines.)
Decomposition of A016096 - 9997 dots.

Decomposition of 3n + 2

3D graph (WebGL) / 2D graph - First 500 terms
3n+2.
A016789(n) = A000000(n) * A000000(n) + 3
Download CSV of the decomposition of 3n + 2 (10000 lines.)
Decomposition of 3n + 2 - 9999 dots.

Decomposition of 4n + 2

3D graph (WebGL) / 2D graph - First 500 terms
Numbers congruent to 2 mod 4: a(n) = 4n+2.
A016825(n) = A000000(n) * A000000(n) + 4
Download CSV of the decomposition of 4n + 2 (10000 lines.)
Decomposition of 4n + 2 - 9999 dots.