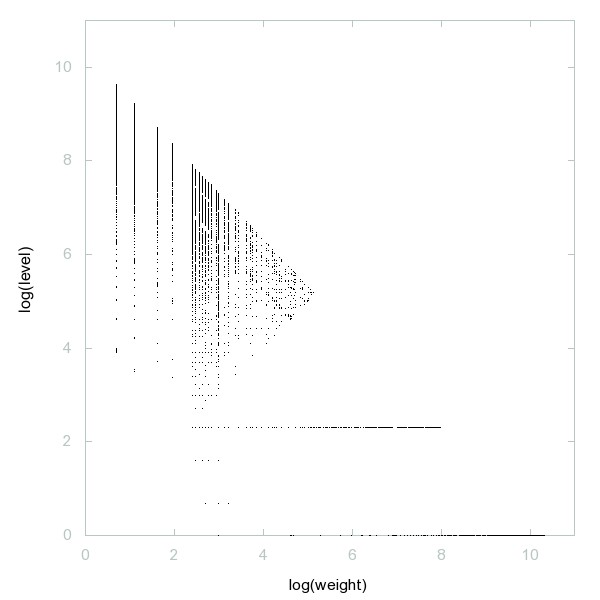
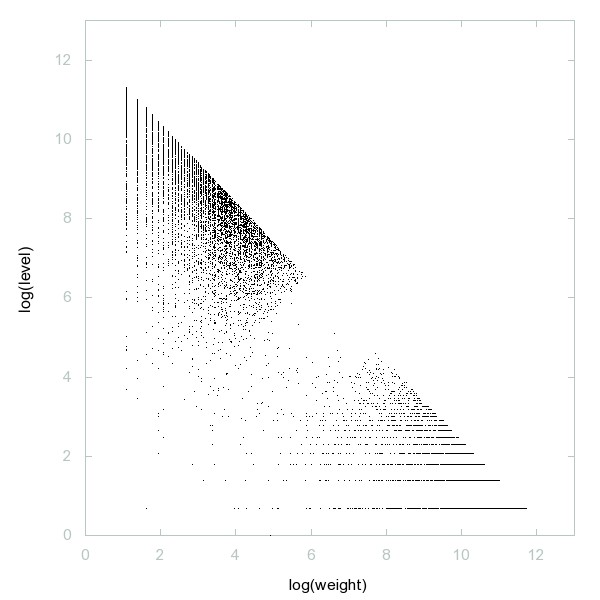
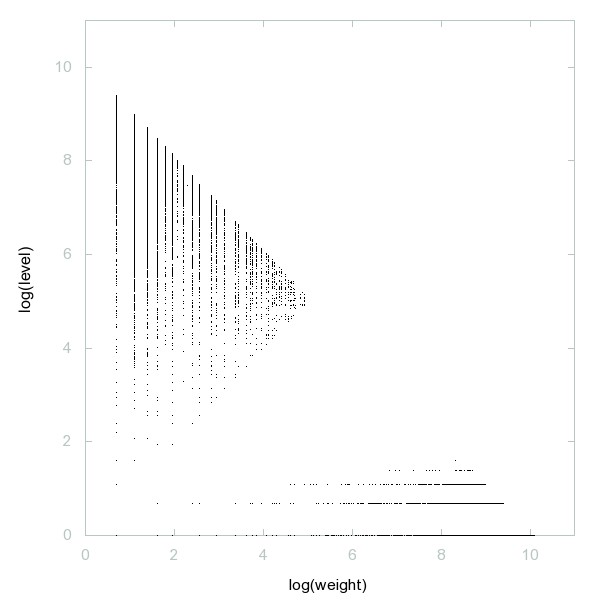
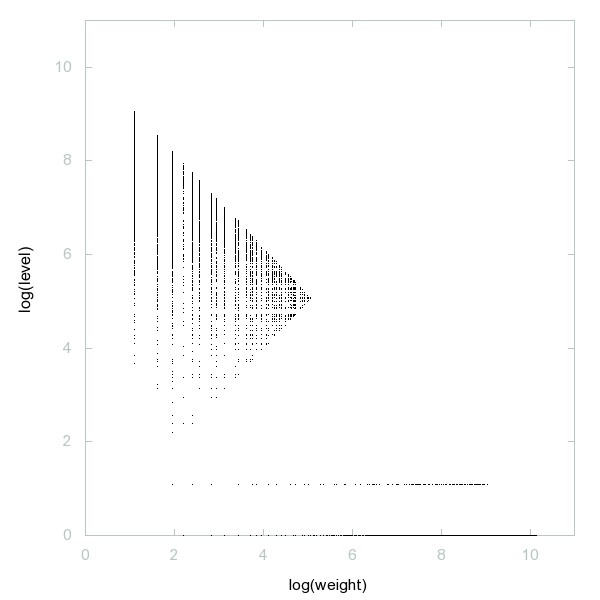
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of A011539

3D graph (WebGL) / 2D graph - First 500 terms
"9ish numbers": decimal representation contains at least one nine.
A011539(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A011539 (9999 lines.)
Decomposition of A011539 - 9997 dots.

Decomposition of A011540

3D graph (WebGL) / 2D graph - First 500 terms
Numbers that contain a 0.
A011540(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A011540 (9999 lines.)
Decomposition of A011540 - 9996 dots.

Decomposition of A011775

3D graph (WebGL) / 2D graph - First 500 terms
Numbers n such that n divides phi(n) * sigma(n).
A011775(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A011775 (9999 lines.)
Decomposition of A011775 - 9997 dots.

Decomposition of A013916

3D graph (WebGL) / 2D graph - First 500 terms
Numbers n such that the sum of the first n primes is prime.
A013916(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A013916 (9999 lines.)
Decomposition of A013916 - 9993 dots.

Decomposition of A013917

3D graph (WebGL) / 2D graph - First 500 terms
a(n) is prime and sum of all primes <= a(n) is prime.
A013917(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A013917 (9999 lines.)
Decomposition of A013917 - 9993 dots.

Decomposition of A013939

3D graph (WebGL) / 2D graph - First 500 terms
Partial sums of sequence A001221 (number of distinct primes dividing n).
A013939(n) = A000000(n) * A000000(n) + A001221(n)
Download CSV of the decomposition of A013939 (9999 lines.)
Decomposition of A013939 - 9995 dots.

Decomposition of A014011

3D graph (WebGL) / 2D graph - First 500 terms
Defined by a chi-inequality greedy algorithm.
A014011(n) = A000000(n) * A000000(n) + A226390(n)
Download CSV of the decomposition of A014011 (9999 lines.)
Decomposition of A014011 - 9995 dots.

Decomposition of Odd nonprimes

3D graph (WebGL) / 2D graph - First 500 terms
Odd nonprimes.
A014076(n) = A000000(n) * A000000(n) + A067970(n)
Download CSV of the decomposition of Odd nonprimes (9999 lines.)
Decomposition of Odd nonprimes - 9997 dots.

Decomposition of A014090

3D graph (WebGL) / 2D graph - First 500 terms
Numbers that are not the sum of a square and a prime.
A014090(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A014090 (9999 lines.)
Decomposition of A014090 - 9996 dots.

Decomposition of A014092

3D graph (WebGL) / 2D graph - First 500 terms
Numbers that are not the sum of 2 primes.
A014092(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A014092 (9999 lines.)
Decomposition of A014092 - 9995 dots.