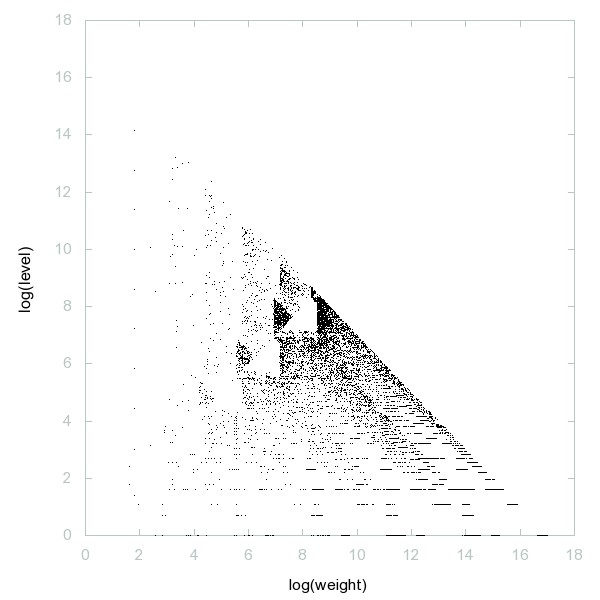
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of Palindromes in base 3

3D graph (WebGL) / 2D graph - First 500 terms
Palindromes in base 3 (written in base 10).
A014190(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of Palindromes in base 3 (9999 lines.)
Decomposition of Palindromes in base 3 - 9995 dots.

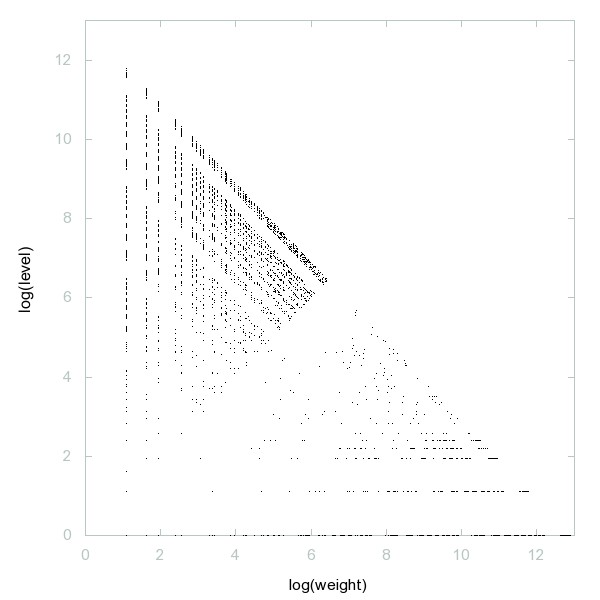
Decomposition of Palindromes in base 4

3D graph (WebGL) / 2D graph - First 500 terms
Palindromes in base 4 (written in base 10).
A014192(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of Palindromes in base 4 (9999 lines.)
Decomposition of Palindromes in base 4 - 9993 dots.

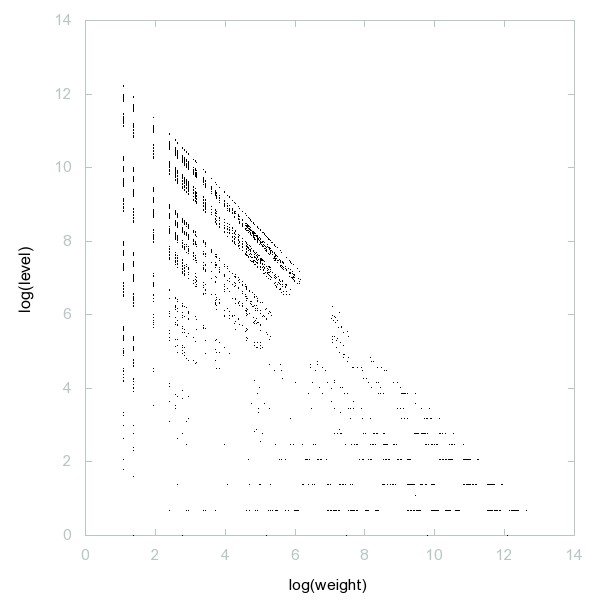
Decomposition of A014261

3D graph (WebGL) / 2D graph - First 500 terms
Numbers that contain odd digits only.
A014261(n) = A000000(n) * A000000(n) + A164898(n)
Download CSV of the decomposition of A014261 (9999 lines.)
Decomposition of A014261 - 9992 dots.

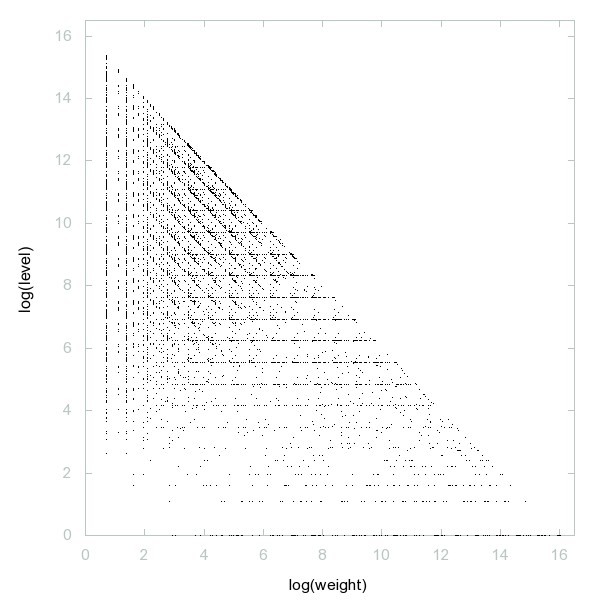
Decomposition of A014263

3D graph (WebGL) / 2D graph - First 500 terms
Numbers that contain even digits only.
A014263(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A014263 (9999 lines.)
Decomposition of A014263 - 9991 dots.

Decomposition of A014312

3D graph (WebGL) / 2D graph - First 500 terms
Numbers with exactly 4 ones in binary expansion.
A014312(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A014312 (9999 lines.)
Decomposition of A014312 - 9998 dots.

Decomposition of A014313

3D graph (WebGL) / 2D graph - First 500 terms
Numbers with exactly 5 ones in binary expansion.
A014313(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A014313 (9999 lines.)
Decomposition of A014313 - 9998 dots.

Decomposition of A014439

3D graph (WebGL) / 2D graph - First 500 terms
Differences between two positive cubes in exactly 1 way.
A014439(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A014439 (9999 lines.)
Decomposition of A014439 - 9997 dots.

Decomposition of Average of twin prime pairs

3D graph (WebGL) / 2D graph - First 500 terms
Average of twin prime pairs.
A014574(n) = A000000(n) * A000000(n) + A053319(n)
Download CSV of the decomposition of Average of twin prime pairs (9999 lines.)
Decomposition of Average of twin prime pairs - 9995 dots.

Decomposition of 3-almost primes

3D graph (WebGL) / 2D graph - First 500 terms
Numbers that are the product of exactly three (not necessarily distinct) primes.
A014612(n) = A130650(n) * A184753(n) + A114403(n)
Download CSV of the decomposition of 3-almost primes (10000 lines.)
Decomposition of 3-almost primes - 9998 dots.

Decomposition of 4-almost primes

3D graph (WebGL) / 2D graph - First 500 terms
Numbers that are products of 4 primes (these numbers are sometimes called "4-almost primes", a generalization of semiprimes).
A014613(n) = A000000(n) * A000000(n) + A114404(n)
Download CSV of the decomposition of 4-almost primes (9999 lines.)
Decomposition of 4-almost primes - 9997 dots.