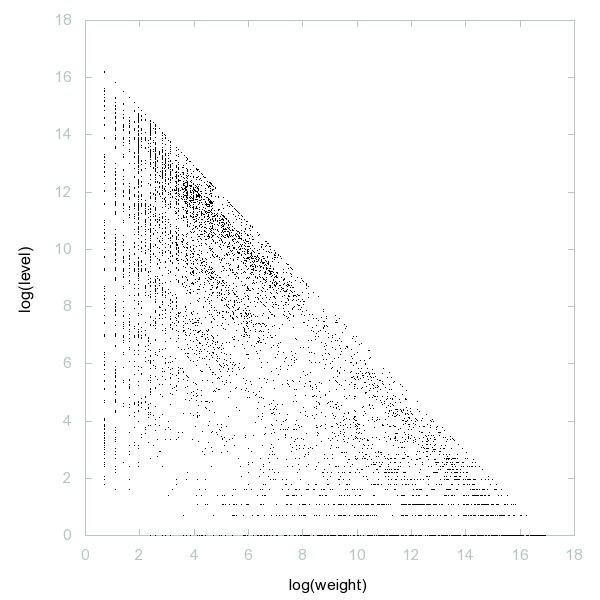
Decomposition of A101594
Numbers with exactly two distinct decimal digits, neither of which is 0.
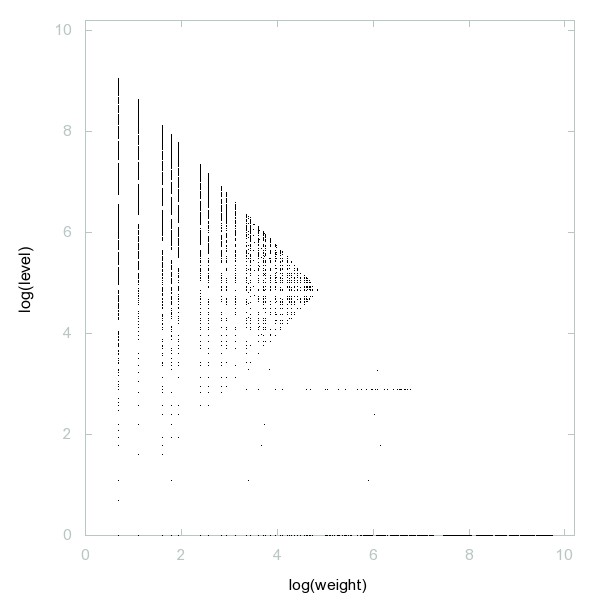
Decomposition of A102487
Numbers in base-12 representation that can be written with decimal digits.
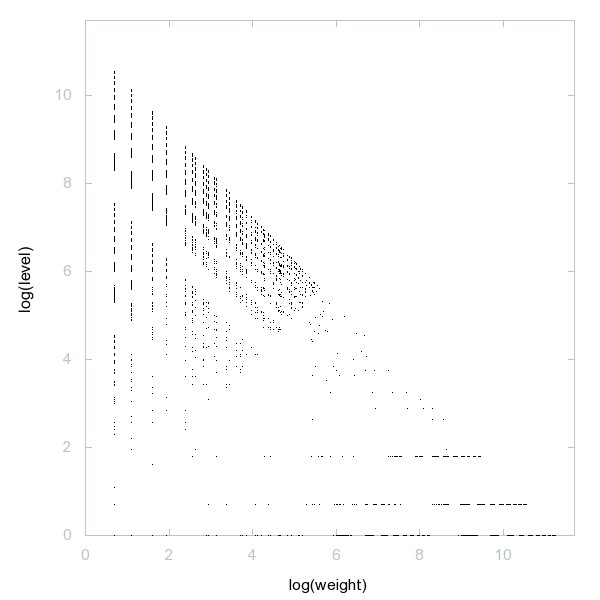
Decomposition of A102491
Numbers whose base-20 representation can be written with decimal digits.
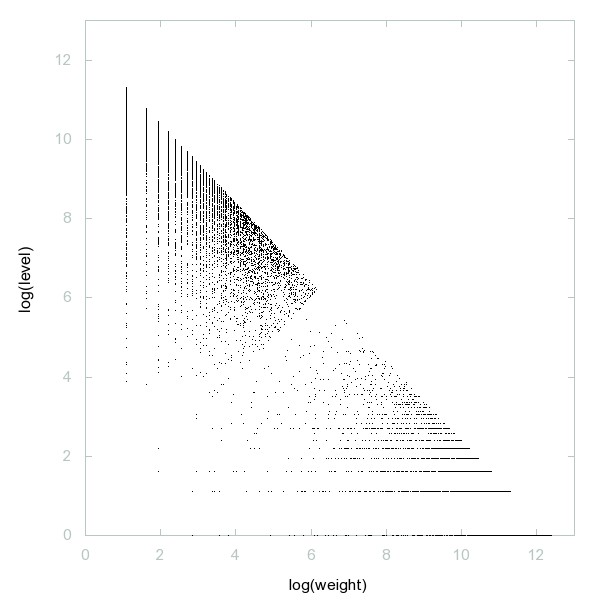
Decomposition of A103664
Primes p such that the number of divisors of p-1 is less than the number of divisors of p+1.
Decomposition of Ramanujan primes
Ramanujan primes R_n: a(n) is the smallest number such that if x >= a(n), then pi(x) - pi(x/2) >= n, where pi(x) is the number of primes <= x.
Decomposition of A105184
Primes that can be written as concatenation of two primes in decimal representation.
Decomposition of A105441
Numbers with at least two odd prime factors (not necessarily distinct).
Decomposition of A105571
Numbers m such that m - 2 and m + 2 are semiprimes.
Decomposition of Belgian-0 numbers
Belgian-0 numbers.
Decomposition of A106349
Primes indexed by semiprimes.