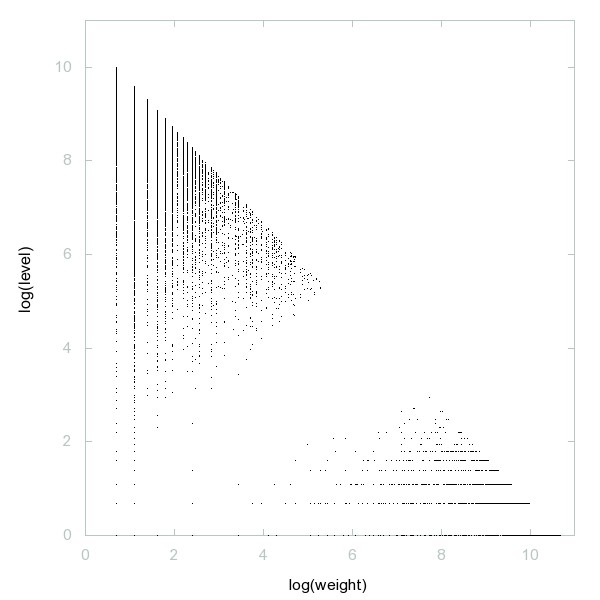
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of A092620

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers with exactly one prime digit.
A092620(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A092620 (9999 lines.)
Decomposition of A092620 - 9996 dots.

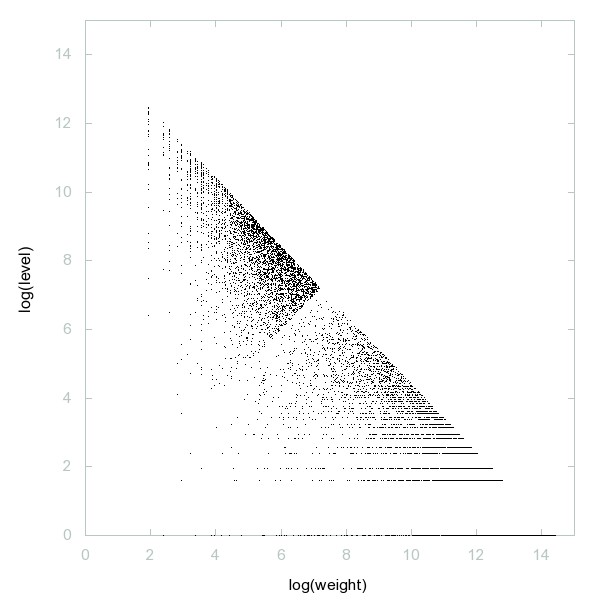
Decomposition of A092621

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes with exactly one prime digit.
A092621(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A092621 (9999 lines.)
Decomposition of A092621 - 9995 dots.

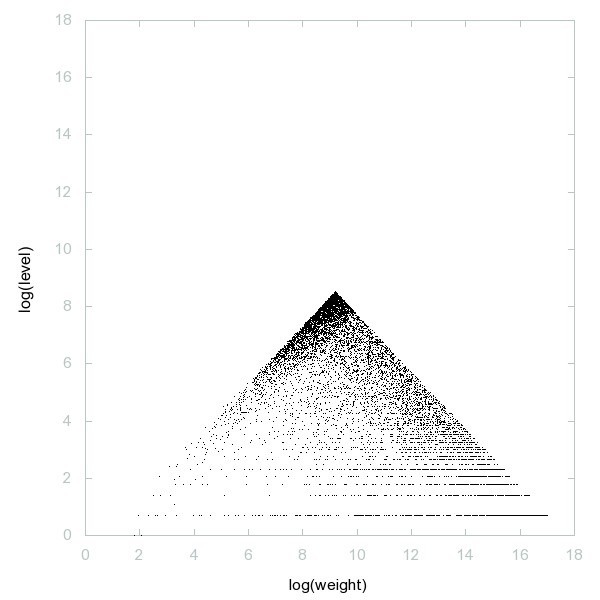
Decomposition of A092671

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that there exists a solution to the equation 1 = 1/x_1 + ... + 1/x_k (for any k), 0 < x_1 < ... < x_k = n.
A092671(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A092671 (9999 lines.)
Decomposition of A092671 - 9997 dots.

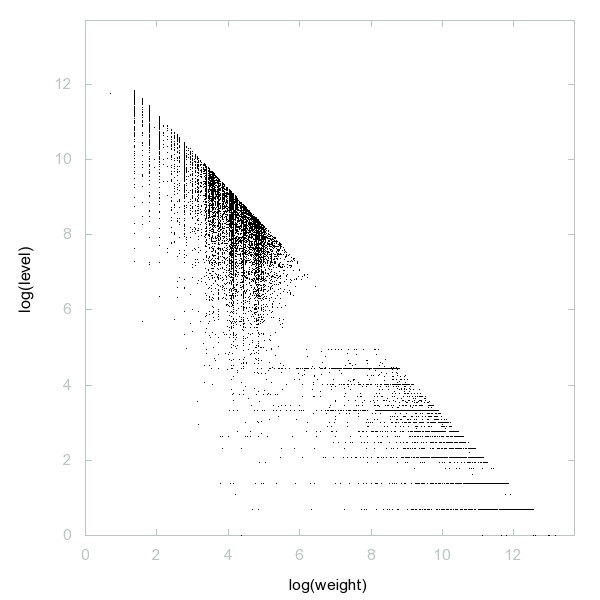
Decomposition of A092968

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that 2n^2 + 11 is a prime.
A092968(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A092968 (9999 lines.)
Decomposition of A092968 - 9996 dots.

Decomposition of A093641

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers of form 2^i * prime(j), i>=0, j>0, together with 1.
A093641(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A093641 (9999 lines.)
Decomposition of A093641 - 9997 dots.

Decomposition of A094524

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes of form 3*prime(n) + 2.
A094524(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A094524 (9999 lines.)
Decomposition of A094524 - 9997 dots.

Decomposition of A094589

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
a(1) = 1; a(n+1) = a(n) + (largest element of {a} <= n).
A094589(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A094589 (9999 lines.)
Decomposition of A094589 - 9995 dots.

Decomposition of A094619

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Fundamental discriminants of real quadratic number fields with class number 2.
A094619(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A094619 (9999 lines.)
Decomposition of A094619 - 9998 dots.

Decomposition of A095050

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers such that all ten digits are needed to write all positive divisors in decimal representation.
A095050(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A095050 (9999 lines.)
Decomposition of A095050 - 9998 dots.

Decomposition of A095301

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that there is some k < n with n*sigma(k) = k*sigma(n).
A095301(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A095301 (9999 lines.)
Decomposition of A095301 - 9998 dots.