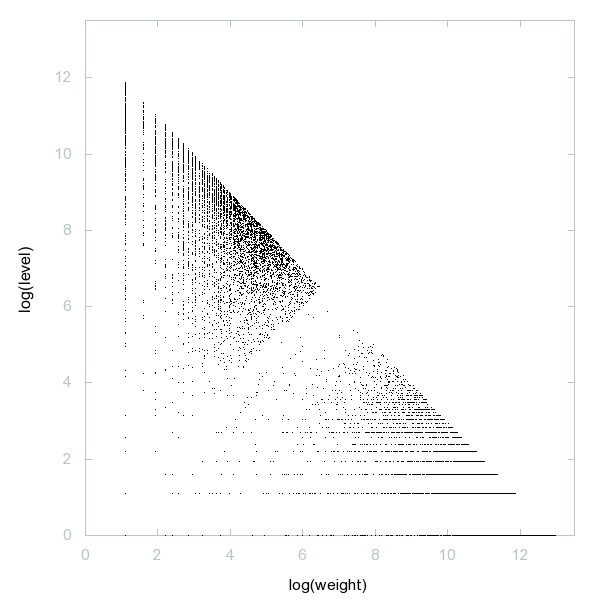
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of A074822

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes p such that p + 4 is prime and p == 9 (mod 10) or primes for which the weight is equal to 5.
A074822(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A074822 (9999 lines.)
Decomposition of A074822 - 9996 dots.

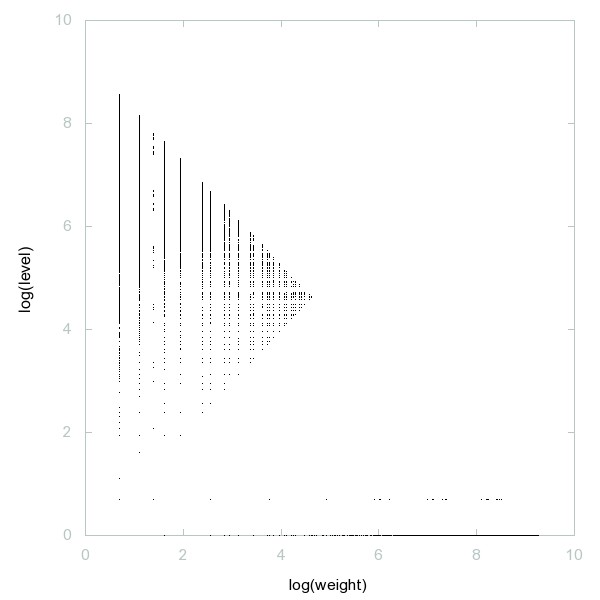
Decomposition of A074832

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes whose binary reversal is also prime.
A074832(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A074832 (9999 lines.)
Decomposition of A074832 - 9997 dots.

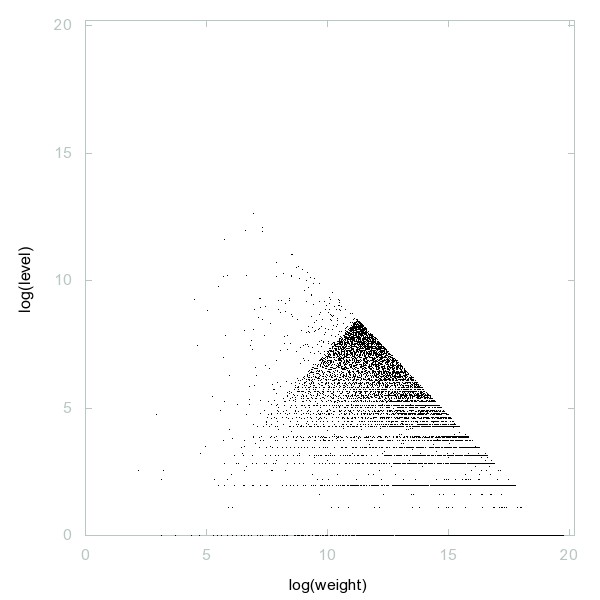
Decomposition of A074940

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers having at least one 2 in their ternary representation.
A074940(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A074940 (9999 lines.)
Decomposition of A074940 - 9998 dots.

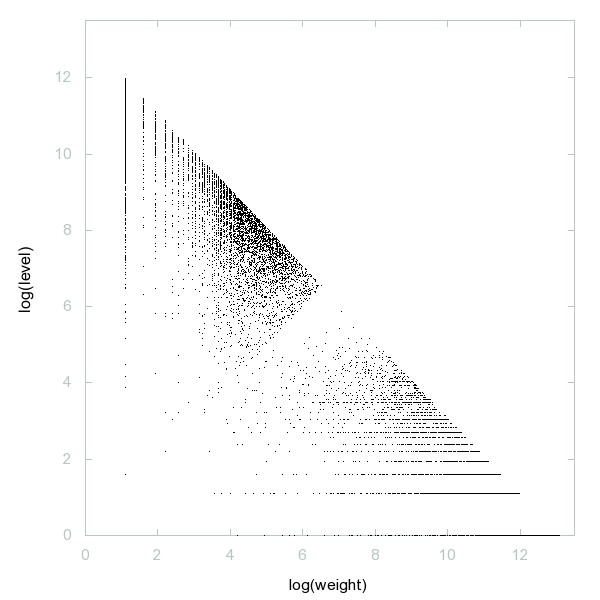
Decomposition of A075109

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Odd perfect powers.
A075109(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A075109 (9999 lines.)
Decomposition of A075109 - 9995 dots.

Decomposition of A075432

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes with no squarefree neighbors.
A075432(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A075432 (9999 lines.)
Decomposition of A075432 - 9997 dots.

Decomposition of A075584

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes p such that the number of distinct prime divisors of all composite numbers between p and the next prime is 4.
A075584(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A075584 (9999 lines.)
Decomposition of A075584 - 9997 dots.

Decomposition of A075587

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes p such that the number of distinct prime divisors of all composite numbers between p and the next prime is 7.
A075587(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A075587 (9999 lines.)
Decomposition of A075587 - 9998 dots.

Decomposition of A075592

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that number of distinct prime divisors of n is a divisor of n.
A075592(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A075592 (9999 lines.)
Decomposition of A075592 - 9998 dots.

Decomposition of A076056

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes which when read backwards are composite numbers.
A076056(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A076056 (9999 lines.)
Decomposition of A076056 - 9999 dots.

Decomposition of A076533

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n such that sum of the distinct prime factors of phi(n) = sum of the distinct prime factors of sigma(n).
A076533(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A076533 (9999 lines.)
Decomposition of A076533 - 9993 dots.