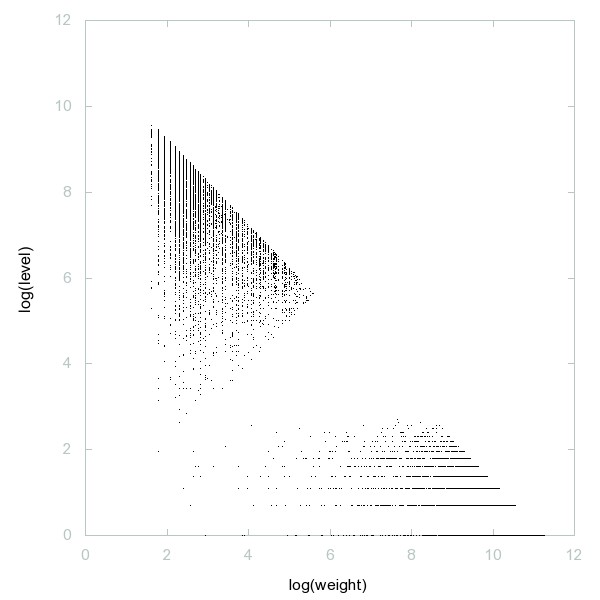
Decomposition of A056233
Form an array with 3 rows: row 1 begins with 1; all rows are increasing; each entry is sum of 2 entries above it; each number appears at most once; smallest unused number is appended to first row if possible. Sequence gives row 3.
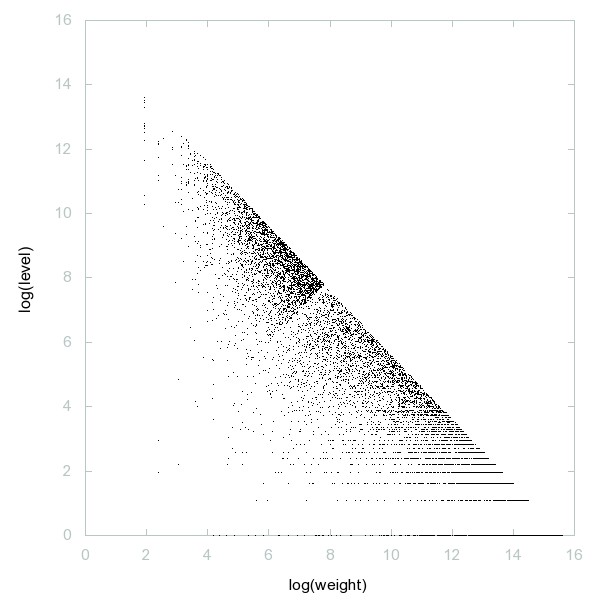
Decomposition of A056234
Form an array with 3 rows: row 1 begins with 1; all rows are increasing; each entry is sum of 2 entries above it; each number appears at most once; smallest unused number is appended to first row if possible. Sequence gives numbers not used.
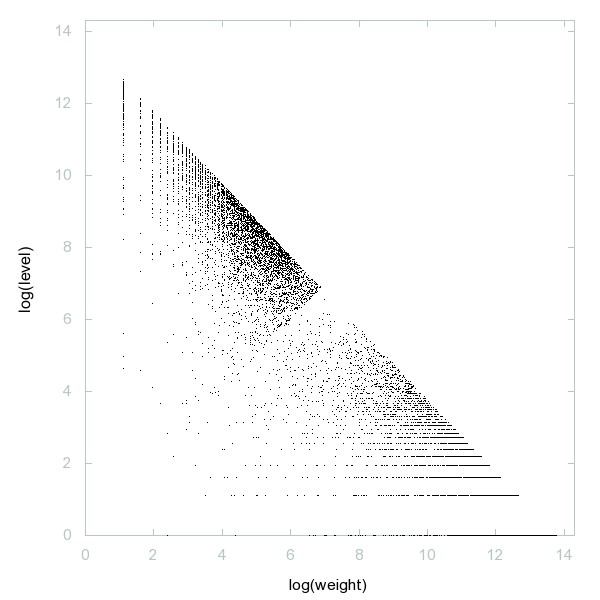
Decomposition of A056524
Palindromes with even number of digits.
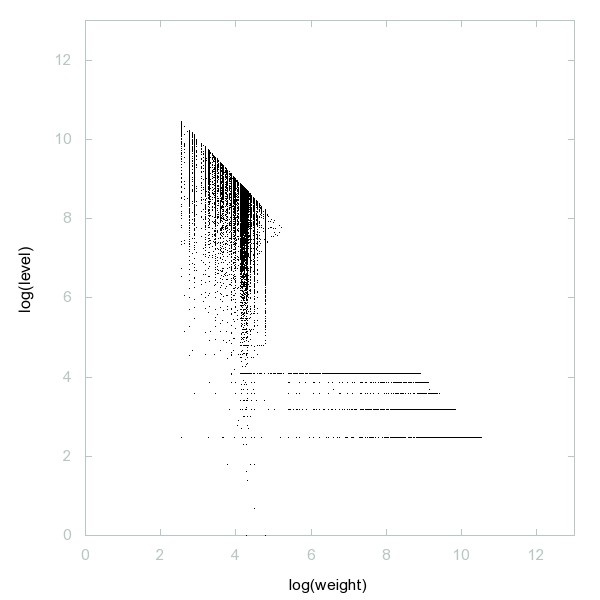
Decomposition of Naught-y primes
Naught-y primes, primes with noughts (or zeros).
Decomposition of A056809
Numbers n such that n, n+1 and n+2 are products of two primes.
Decomposition of A056815
Primes with prime "look and say" descriptions.
Decomposition of A056866
Orders of non-solvable groups, i.e. numbers which are not solvable numbers.
Decomposition of Nilpotent numbers
Nilpotent numbers: n such that every group of order n is nilpotent.
Decomposition of A056868
Numbers which are not nilpotent numbers.
Decomposition of A056874
Primes of form x^2+xy+3y^2, discriminant -11.