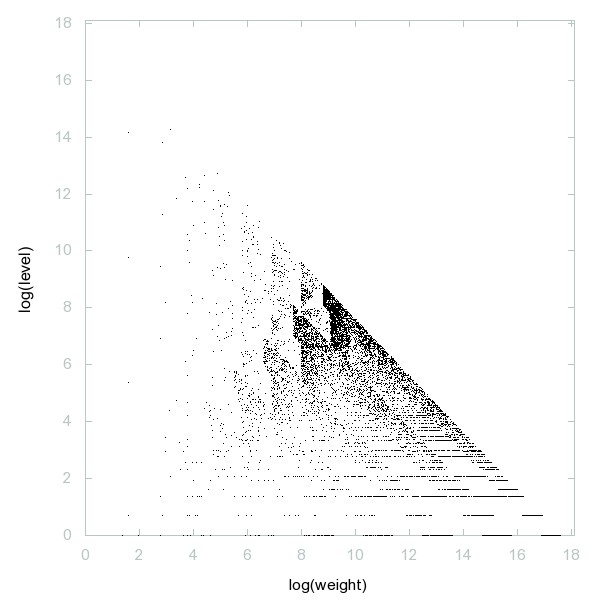
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of A133870

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Primes of the form 32*n + 1.
A133870(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A133870 (9999 lines.)
Decomposition of A133870 - 9998 dots.

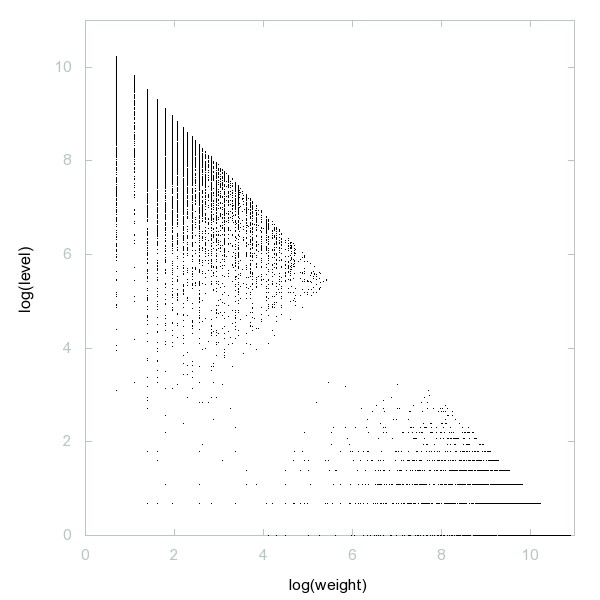
Decomposition of A134027

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Nonnegative numbers that are palindromes in balanced ternary representation.
A134027(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A134027 (9999 lines.)
Decomposition of A134027 - 9995 dots.

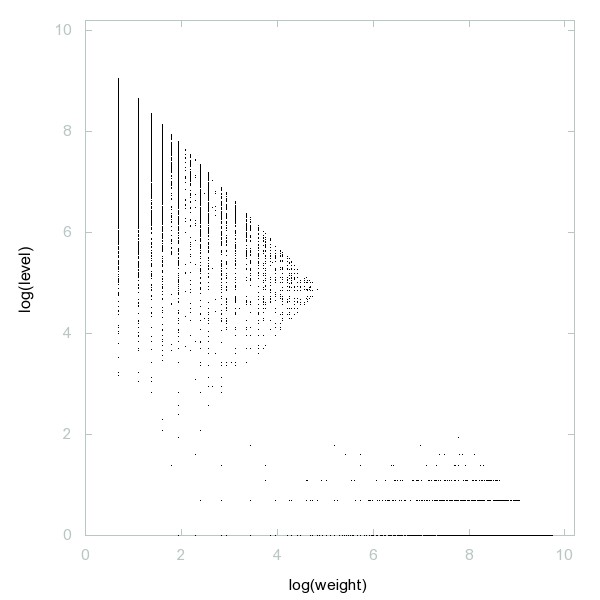
Decomposition of A134333

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers n whose number of prime factors (counted with multiplicity) is a prime factor of n.
A134333(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A134333 (9999 lines.)
Decomposition of A134333 - 9997 dots.

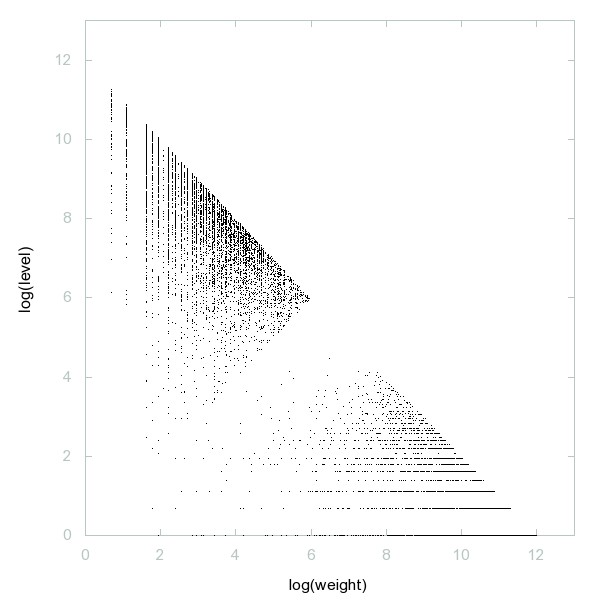
Decomposition of A134334

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers which are not divisible by the number of their prime factors (counted with multiplicity).
A134334(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A134334 (9999 lines.)
Decomposition of A134334 - 9998 dots.

Decomposition of A134344

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Composite numbers such that the arithmetic mean of their prime factors (counted with multiplicity) is prime .
A134344(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A134344 (9999 lines.)
Decomposition of A134344 - 9997 dots.

Decomposition of A134376

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers whose sum of prime factors (counted with multiplicity) is not prime.
A134376(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A134376 (9999 lines.)
Decomposition of A134376 - 9996 dots.

Decomposition of A134600

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Composite numbers such that the square mean of their prime factors is an integer (where the prime factors are taken with multiplicity and the square mean of c and d is sqrt((c^2+d^2)/2)).
A134600(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A134600 (9999 lines.)
Decomposition of A134600 - 9995 dots.

Decomposition of A134602

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Composite numbers such that the square mean of their prime factors is a nonprime integer (where the prime factors are taken with multiplicity and the square mean of c and d is sqrt((c^2+d^2)/2)).
A134602(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A134602 (9999 lines.)
Decomposition of A134602 - 9998 dots.

Decomposition of A134605

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Composite numbers such that the square root of the sum of squares of their prime factors is an integer.
A134605(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A134605 (9999 lines.)
Decomposition of A134605 - 9995 dots.

Decomposition of A134616

3D graph (WebGL) / 2D graph - First 500 terms / Generation of 3D graph
Numbers such that the sum of squares of their prime factors (taken with multiplicity) is a prime.
A134616(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A134616 (9999 lines.)
Decomposition of A134616 - 9997 dots.