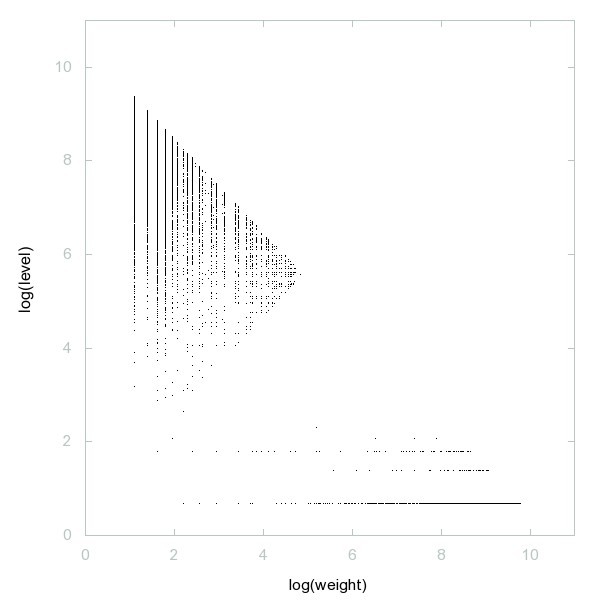
Decomposition into weight × level + jump - all 2D graphs

Home

Decomposition of A005244

3D graph (WebGL) / 2D graph - First 500 terms
A self-generating sequence: start with 2 and 3, take all products of any 2 previous elements, subtract 1 and adjoin them to the sequence.
A005244(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A005244 (9999 lines.)
Decomposition of A005244 - 9994 dots.

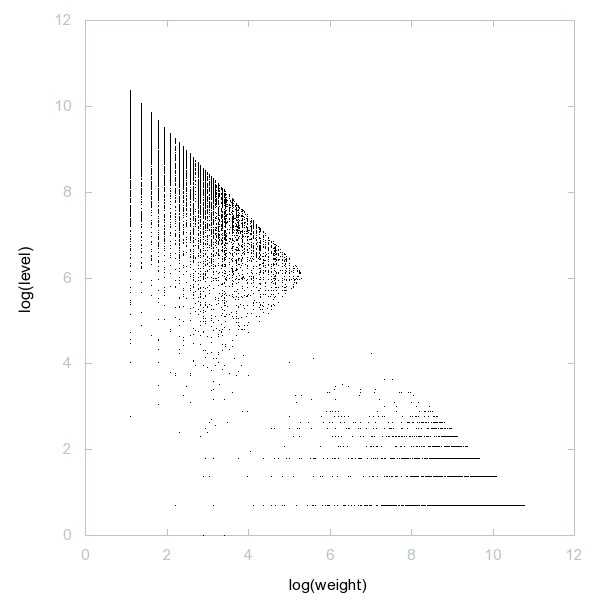
Decomposition of Nontotients

3D graph (WebGL) / 2D graph - First 500 terms
Nontotients: even n such that phi(m) = n has no solution.
A005277(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of Nontotients (9999 lines.)
Decomposition of Nontotients - 9998 dots.

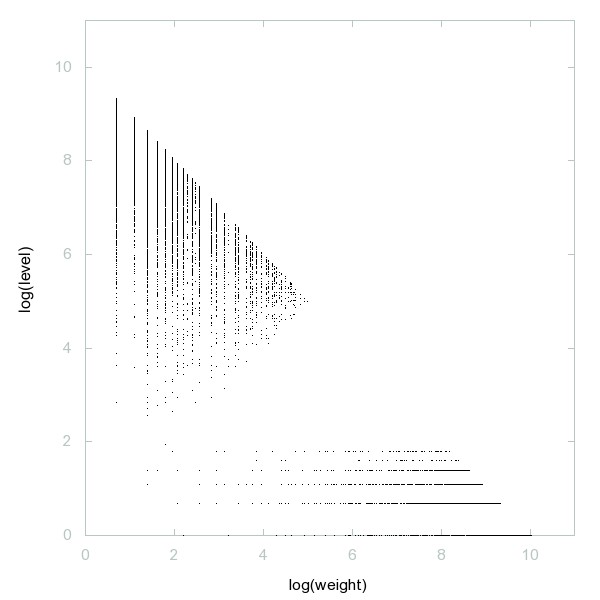
Decomposition of Noncototients

3D graph (WebGL) / 2D graph - First 500 terms
Noncototients: n such that x - phi(x) = n has no solution.
A005278(n) = A000000(n) * A000000(n) + A083536(n)
Download CSV of the decomposition of Noncototients (9999 lines.)
Decomposition of Noncototients - 9998 dots.

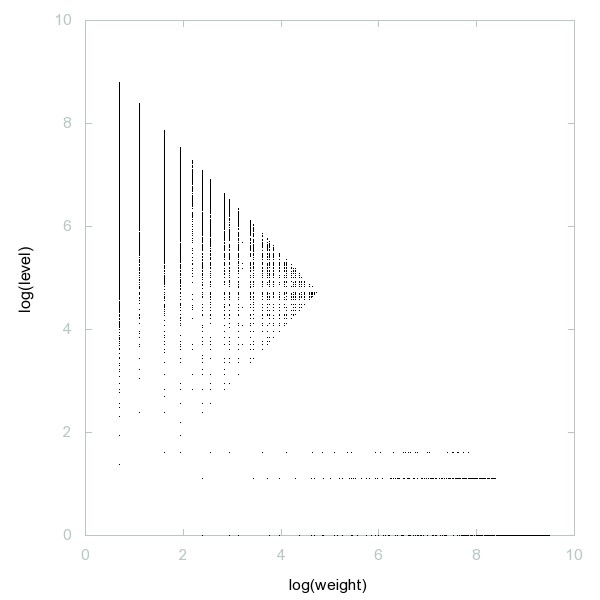
Decomposition of A005279

3D graph (WebGL) / 2D graph - First 500 terms
Numbers having divisors d,e with d < e < 2d.
A005279(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A005279 (9999 lines.)
Decomposition of A005279 - 9998 dots.

Decomposition of Niven numbers

3D graph (WebGL) / 2D graph - First 500 terms
Niven (or Harshad) numbers: numbers that are divisible by the sum of their digits.
A005349(n) = A000000(n) * A000000(n) + A082516(n)
Download CSV of the decomposition of Niven numbers (10000 lines.)
Decomposition of Niven numbers - 9997 dots.

Decomposition of A005381

3D graph (WebGL) / 2D graph - First 500 terms
Numbers n such that n and n-1 are composite.
A005381(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A005381 (9999 lines.)
Decomposition of A005381 - 9998 dots.

Decomposition of A005382

3D graph (WebGL) / 2D graph - First 500 terms
Primes p such that 2p-1 is also prime.
A005382(n) = A000000(n) * A000000(n) + A074258(n)
Download CSV of the decomposition of A005382 (9999 lines.)
Decomposition of A005382 - 9994 dots.

Decomposition of A005383

3D graph (WebGL) / 2D graph - First 500 terms
Numbers n such that both n and (n+1)/2 are primes.
A005383(n) = A000000(n) * A000000(n) + A000000(n)
Download CSV of the decomposition of A005383 (9999 lines.)
Decomposition of A005383 - 9994 dots.

Decomposition of Sophie Germain primes

3D graph (WebGL) / 2D graph - First 500 terms
Sophie Germain primes p: 2p+1 is also prime.
A005384(n) = A000000(n) * A000000(n) + A074259(n)
Download CSV of the decomposition of Sophie Germain primes (10000 lines.)
Decomposition of Sophie Germain primes - 9995 dots.

Decomposition of Safe primes

3D graph (WebGL) / 2D graph - First 500 terms
Safe primes p: (p-1)/2 is also prime.
A005385(n) = A000000(n) * A000000(n) + A059322(n)
Download CSV of the decomposition of Safe primes (9999 lines.)
Decomposition of Safe primes - 9995 dots.